题目内容
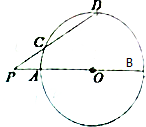 如图所示,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7
如图所示,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7| 1 |
| 3 |
考点:与圆有关的比例线段
专题:直线与圆
分析:由切割线定理得PC•PD=PA•PB,设圆半径为r,则6(6+7
)=(12-r)(12+r),由此能求出AB的长.
| 1 |
| 3 |
解答:
解:设圆半径为r,
∵⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,
∴PC•PD=PA•PB,
∵PC=6,CD=7
,PO=12,
∴6(6+7
)=(12-r)(12+r),
解得r=8,
∴AB=2r=16.
故答案为:16.
∵⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,
∴PC•PD=PA•PB,
∵PC=6,CD=7
| 1 |
| 3 |
∴6(6+7
| 1 |
| 3 |
解得r=8,
∴AB=2r=16.
故答案为:16.
点评:本题考查圆的直径的求法,是基础题,解题时要认真审题,注意切割线定理的合理运用.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
在等腰△ABC中,∠A为顶角,若sinB=
,cosA的值为( )
| 2 |
| 3 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
设全集U={x∈Z|-2<x<4},A={-1,0},B={0,1,2},则(∁UA)∩B=( )
| A、{0} |
| B、{-2,-1} |
| C、{1,2} |
| D、{0,1,2} |
设a,b∈R且a+b=3,b>0,则当
+
取得最小值时,实数a的值是( )
| 1 |
| 3|a| |
| |a| |
| b |
A、
| ||||
B、-
| ||||
C、-
| ||||
| D、3 |
已知函数f(x)=|x+a|在(-∞,-1)上是单调函数,则a的取值范围是( )
| A、(-∞,1] |
| B、(-∞,-1] |
| C、[-1,+∞) |
| D、[1,+∞) |
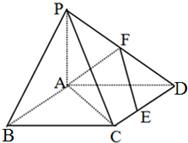 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,且PA=PD,点F是棱PD的中点,点E为CD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,且PA=PD,点F是棱PD的中点,点E为CD的中点.