题目内容
投掷四枚不同的金属硬币A、B、C、D,假定A、B两枚正面向上的概率均为
,另两枚C、D为非均匀硬币,正面向上的概率均为a(0<a<1),把这四枚硬币各投掷一次,设X表示正面向上的枚数.
(1)若A、B出现一枚正面向上一枚反面向上与C、D出现两枚正面均向上的概率相等,求a的值;
(2)求X的分布列及数学期望(用a表示).
| 1 |
| 2 |
(1)若A、B出现一枚正面向上一枚反面向上与C、D出现两枚正面均向上的概率相等,求a的值;
(2)求X的分布列及数学期望(用a表示).
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式,离散型随机变量及其分布列
专题:概率与统计
分析:(1)由题意,得2×
(1-
)=a2,由此能求出a.
(2)由已知得X=0,1,2,3,4,分别求出相应的概率,由此能求出X的分布列及数学期望(用a表示).
| 1 |
| 2 |
| 1 |
| 2 |
(2)由已知得X=0,1,2,3,4,分别求出相应的概率,由此能求出X的分布列及数学期望(用a表示).
解答:
解:(1)∵A、B出现一枚正面向上一枚反面向上与C、D出现两枚正面均向上的概率相等,
∴由题意,得2×
(1-
)=a2,
解得a=
.
(2)由已知得X=0,1,2,3,4,
P(X=0)=
(1-
)2
(1-a)2=
(1-a)2,
P(X=1)=
×
×(1-
)
(1-a)2+
(1-
)2
a(1-a)=
(1-a),
P(X=2)=
(
)2
(1-a)2+
•
(1-
)
a(1-a)+
(1-
)2
a2=
(1+2a-2a2),
P(X=3)=
(
)2
a(1-a)+
•
(1-
)
a2=
,
P(X=4)=
(
)2
a2=
a2,
∴X的分布列为:
EX=1×
(1-a)+2×
(1+2a-2a2)+3×
+4×
a2=2a+1.
∴由题意,得2×
| 1 |
| 2 |
| 1 |
| 2 |
解得a=
| ||
| 2 |
(2)由已知得X=0,1,2,3,4,
P(X=0)=
| C | 0 2 |
| 1 |
| 2 |
| C | 0 2 |
| 1 |
| 4 |
P(X=1)=
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 0 2 |
| C | 0 2 |
| 1 |
| 2 |
| C | 1 2 |
| 1 |
| 2 |
P(X=2)=
| C | 2 2 |
| 1 |
| 2 |
| C | 0 2 |
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 2 |
| C | 0 2 |
| 1 |
| 2 |
| C | 2 2 |
| 1 |
| 4 |
P(X=3)=
| C | 2 2 |
| 1 |
| 2 |
| C | 1 2 |
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 2 2 |
| a |
| 2 |
P(X=4)=
| C | 2 2 |
| 1 |
| 2 |
| C | 2 2 |
| 1 |
| 4 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 2 |
| 1 |
| 4 |
| a |
| 2 |
| 1 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
命题p:5是奇数,q:7是偶数,则下列说法中正确的是( )
| A、p或q为真 | B、p且q为真 |
| C、非p为真 | D、非q为假 |
已知全集U=R,集合A={x|2x>1},B={x|log2x>2},则A∩B=( )
| A、{x|x>0} |
| B、{x|x<-1或x>0} |
| C、{x|x>4} |
| D、{x|-1≤x≤4} |
已知F1,F2是椭圆和双曲线的公共焦点,M是它们的一个公共点,且∠F1MF2=
,则椭圆和双曲线的离心率的倒数之和的最大值为( )
| π |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
| D、4 |
已知函数y=f(x)的图象如图,则满足f(
)•f(5)≤0的x取值范围为( )
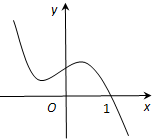
| 2x+1 |
| x-1 |

| A、[-2,1) |
| B、[-1,1] |
| C、[1,2] |
| D、[2,3] |
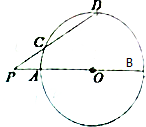 如图所示,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7
如图所示,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7