题目内容
已知函数f(x)=|x+a|在(-∞,-1)上是单调函数,则a的取值范围是( )
| A、(-∞,1] |
| B、(-∞,-1] |
| C、[-1,+∞) |
| D、[1,+∞) |
考点:函数单调性的性质
专题:计算题,函数的性质及应用
分析:首先化简f(x),求出单调区间,则函数f(x)在(-∞,-1)上是单调递减函数,则有-a≥-1,解得a即可得到范围.
解答:
解:由于函数f(x)=|x+a|=
,
则f(x)的单调增区间为(-a,+∞),单调减区间为(-∞,-a).
由f(x)在(-∞,-1)上是单调函数,即有(-∞,-1)⊆(-∞,-a).
所以-a≥-1,解得a≤1.
故选A.
|
则f(x)的单调增区间为(-a,+∞),单调减区间为(-∞,-a).
由f(x)在(-∞,-1)上是单调函数,即有(-∞,-1)⊆(-∞,-a).
所以-a≥-1,解得a≤1.
故选A.
点评:本题考查了函数的化简及函数的单调性的判断,注意去绝对值时要进行讨论及审题,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合A={x|x2-3x+2≥0},B={x|x≤2,x∈Z},则(CRA)∩B=( )
| A、∅ | B、{1} |
| C、{2} | D、{1,2} |
已知函数y=f(x)的图象如图,则满足f(
)•f(5)≤0的x取值范围为( )
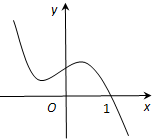
| 2x+1 |
| x-1 |

| A、[-2,1) |
| B、[-1,1] |
| C、[1,2] |
| D、[2,3] |
已知如图程序框图,则输出的i是( )


| A、9 | B、11 | C、13 | D、15 |
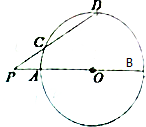 如图所示,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7
如图所示,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7