题目内容
设函数f(x)=
(a∈R).
(1)若f(x)为R上的奇函数,求a的值;
(2)若f(x)在R上为减函数,求a的取值范围.
| a-e x |
| 1+e x |
(1)若f(x)为R上的奇函数,求a的值;
(2)若f(x)在R上为减函数,求a的取值范围.
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)由f(x)为R上的奇函数,得f(0)=0,求出a的值,再验证f(x)是否为R上的奇函数即可;
(2)利用分离常数法化简f(x),由基本初等函数的单调性,求出a的取值范围.
(2)利用分离常数法化简f(x),由基本初等函数的单调性,求出a的取值范围.
解答:
解:(1)∵函数f(x)=
(a∈R),
∴当f(x)为R上的奇函数时,f(0)=0,
即
=0,
解得a=1,
此时f(x)=
是R上的奇函数,
∴a的值是1;
(2)∵f(x)=
=
=
-1,
当f(x)在R上为减函数时,a+1>0,
解得a>-1;
∴a的取值范围是a>-1.
| a-e x |
| 1+e x |
∴当f(x)为R上的奇函数时,f(0)=0,
即
| a-1 |
| 1+1 |
解得a=1,
此时f(x)=
| 1-ex |
| 1+ex |
∴a的值是1;
(2)∵f(x)=
| a-ex |
| 1+ex |
=
| (a+1)-(1+ex) |
| 1+ex |
=
| a+1 |
| 1+ex |
当f(x)在R上为减函数时,a+1>0,
解得a>-1;
∴a的取值范围是a>-1.
点评:本题考查了函数的奇偶性与单调性的应用问题,是基础性题目.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
已知函数y=f(x)的图象如图,则满足f(
)•f(5)≤0的x取值范围为( )
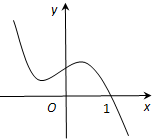
| 2x+1 |
| x-1 |

| A、[-2,1) |
| B、[-1,1] |
| C、[1,2] |
| D、[2,3] |
已知如图程序框图,则输出的i是( )


| A、9 | B、11 | C、13 | D、15 |
设{an}是由正数组成的等比数列,Sn为其前n项和.已知a2a4=1,S3=7,则S5=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
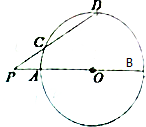 如图所示,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7
如图所示,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7