题目内容
在等腰△ABC中,∠A为顶角,若sinB=
,cosA的值为( )
| 2 |
| 3 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:如图所示,作AD垂直于BC,利用等腰三角形三线合一性质得到AD为角平分线,D为BC中点,在直角三角形ABD中,利用锐角三角函数定义得到cos∠BAD=sinB,再利用二倍角的余弦函数公式求出cos∠BAC的值即可.
解答:
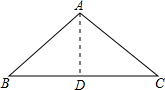 解:如图所示,作AD⊥BC,利用三线合一得到AD平分∠BAC,D为BC中点,
解:如图所示,作AD⊥BC,利用三线合一得到AD平分∠BAC,D为BC中点,
在Rt△ABD中,sinB=
=
,∠B+∠BAD=90°,
∴cos∠BAD=sinB=
,
∵∠BAC=2∠BAD,
∴cos∠BAC=cos2∠BAD=2cos2∠BAD-1=-
,
故选:A.
 解:如图所示,作AD⊥BC,利用三线合一得到AD平分∠BAC,D为BC中点,
解:如图所示,作AD⊥BC,利用三线合一得到AD平分∠BAC,D为BC中点,在Rt△ABD中,sinB=
| AD |
| AB |
| 2 |
| 3 |
∴cos∠BAD=sinB=
| 2 |
| 3 |
∵∠BAC=2∠BAD,
∴cos∠BAC=cos2∠BAD=2cos2∠BAD-1=-
| 1 |
| 9 |
故选:A.
点评:此题考查了同角三角函数基本关系的运用,以及锐角三角函数定义,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
直线a在平面α内,可以记作( )
| A、a∈α | B、a?α |
| C、α∈a | D、α?a |
已知实数x,y满足
,若z=y-ax(a≠0)取得的最优解(x,y)有无数个,则a的值为( )
|
| A、2 | B、1 | C、1或2 | D、-1 |
命题p:5是奇数,q:7是偶数,则下列说法中正确的是( )
| A、p或q为真 | B、p且q为真 |
| C、非p为真 | D、非q为假 |
已知集合A={x|x2-3x+2≥0},B={x|x≤2,x∈Z},则(CRA)∩B=( )
| A、∅ | B、{1} |
| C、{2} | D、{1,2} |
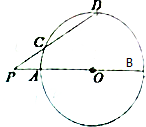 如图所示,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7
如图所示,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7