Question

16．若关于x的不等式x²+mx一4≥0在区间[1，4]上有解．则实数m的最小值是-3．

Answer 1

分析 方程x²+mx-4=0有两个不等实数根，且一正一负，二次不等式x²+mx一4≥0对应的二次函数开口向上，画出图形，结合不等式x²+mx一4≥0在区间[1，4]上有解得到关于m的不等式，求解不等式得答案．

解答 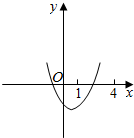解：∵△=m²+16＞0，
∴不等式x²+mx-4≥0对应的二次方程有两不等实数根x₁，x₂，
又x₁x₂=-4＜0，
∴方程x²+mx-4=0有一正根一负根，
要使关于x的不等式x²+mx-4≥0在区间[1，4]上有解，
如图，
则4²+4m-4≥0，即m≥-3．
∴实数m的最小值是-3．
故答案为：-3．

点评 本题考查一元二次方程根的分布与系数间的关系，考查数学转化思想方法，是中档题．