题目内容
一点沿直线运动，如果由始点起经过t秒后的距离为s=
t4-
t3+7t2-8t，则速度为零的时刻是 ．
| 1 |
| 4 |
| 7 |
| 3 |
考点：变化的快慢与变化率
专题：导数的概念及应用
分析：距离对时间的导数为速度，令导数为0，我们可以求出速度为零的时刻．
解答：
解：求导函数s′=t3-7t2+14t-8=（t-1）（t2-6t+8）
令s′=0，可得（t-1）（t2-6t+8）=0
∴t=1．
故答案为：1秒．
令s′=0，可得（t-1）（t2-6t+8）=0
∴t=1．
故答案为：1秒．
点评：本题考查实际问题中导数的意义，把握距离对时间的导数为速度是解题的关键．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
如图，O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足
=
+λ(
+
)，λ∈（0，+∞），则点P的轨迹一定通过△ABC的（ ）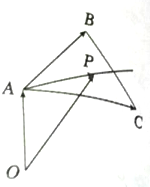
| OP |
| OA |
| ||
|
|
| ||
|
|
| A、外心 | B、内心 | C、重心 | D、垂心 |
若x2＞x1＞1则（ ）
| A、e x1-x2＜lgx1-lgx2 | ||
B、e
| ||
| C、x1 x2＞x2 x1 | ||
| D、x1 x2＜x2 x1 |