题目内容
如图，O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足
=
+λ(
+
)，λ∈（0，+∞），则点P的轨迹一定通过△ABC的（ ）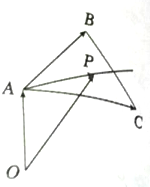
| OP |
| OA |
| ||
|
|
| ||
|
|
| A、外心 | B、内心 | C、重心 | D、垂心 |
考点：向量在几何中的应用
专题：平面向量及应用
分析：先根据
、
分别表示向量
、
方向上的单位向量，确定
-
=
，判断
与∠BAC的角平分线的关系推出选项．
| ||
|
|
| ||
|
|
| AB |
| AC |
| OP |
| OA |
| AP |
| AP |
解答：
解：∵
、
分别表示向量
、
方向上的单位向量，
∴
+
的方向与∠BAC的角平分线重合，
又∵
=
+λ(
+
)可得到
-
=
=λ（
+
）
∴向量
的方向与∠BAC的角平分线重合，
∴一定通过△ABC的内心
故选B．
| ||
|
|
| ||
|
|
| AB |
| AC |
∴
| ||
|
|
| ||
|
|
又∵
| OP |
| OA |
| ||
|
|
| ||
|
|
| OP |
| OA |
| AP |
| ||
|
|
| ||
|
|
∴向量
| AP |
∴一定通过△ABC的内心
故选B．
点评：本题主要考查向量的线性运算和几何意义．属中档题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
已知双曲线C：
-
=1（a＞0，b＞0）的两条渐近线与抛物线y2=2px（p＞0）的准线分别交于A，B两点，O为坐标原点，若双曲线C的离心率为2，△AOB的面积为
，则△AOB的内切圆半径为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
设U=R，集合A={x|x＞0}，B={x∈Z|x2-4≤0}，则下列结论正确的是（ ）
| A、（∁UA）∩B={-2，-1，0} |
| B、（∁UA）∪B=（-∞，0] |
| C、（∁UA）∩B={1，2} |
| D、A∪B=（0，+∞） |