题目内容
14.已知函数$f(x)=\frac{1-x}{{1+{x^2}}}{e^x}$,若f(x1)=f(x2),且x1<x2,关于下列命题:(1)f(x1)>f(-x2);(2)f(x2)>f(-x1);(3)f(x1)>f(-x1);(4)f(x2)>f(-x2).正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 求出函数f(x)的导函数,判断函数的单调性,画出图象,结合椭题意可知x1∈(-∞,0),x2∈(0,1).再证明?x∈(0,1),f(x)<f(-x),数形结合得答案.
解答 解:函数f(x)的定义域为R.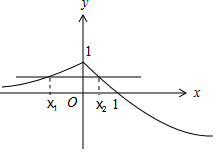
f′(x)=$\frac{-x[(x-1)^{2}+2]}{(1+{x}^{2})^{2}}•{e}^{x}$,
当x<0时,f′(x)>0;当x>0时,f′(x)<0.
∴函数f(x)的单调递增区间为(-∞,0),单调递减区间为(0,+∞).
由f(x1)=f(x2),且x1<x2,可知x1<0,x2>0,
当x<1时,由于$\frac{1-x}{1+{x}^{2}}$>0,ex>0,得到f(x)>0;同理,当x>1时,f(x)<0.
由上可知:x1∈(-∞,0),x2∈(0,1).
下面证明:?x∈(0,1),f(x)<f(-x),
即证$\frac{1-x}{1+{x}^{2}}•{e}^{x}$<$\frac{1+x}{1+{x}^{2}}•{e}^{-x}$.
此不等式等价于$(1-x){e}^{x}-\frac{1+x}{{e}^{x}}$<0.
令g(x)=$(1-x){e}^{x}-\frac{1+x}{{e}^{x}}$,则g′(x)=-xe-x(e2x-1).
当x∈(0,1)时,g′(x)<0,g(x)单调递减,
∴g(x)<g(0)=0.
即$(1-x){e}^{x}-\frac{1+x}{{e}^{x}}$<0.
∴?x∈(0,1),f(x)<f(-x).
由x1∈(-∞,0),可知f(x1)<f(-x2),故(1)错误;
f(x1)>f(-x1),故(3)正确;
由x2∈(0,1),可知f(x2)>f(-x1),故(2)正确;
f(x2)<f(-x2),故(4)错误.
∴正确命题的个数是2个.
故选:B.
点评 本题考查利用导数研究函数的单调性,考查逻辑思维能力与推理运算能力,体现了数形结合的解题思想方法,是中档题.

| A. | ±2$\sqrt{2}$ | B. | ±3 | C. | ±4 | D. | ±2$\sqrt{5}$ |

| A. | 7$+\sqrt{7}$ | B. | 4+4$\sqrt{3}$ | C. | 4+4$\sqrt{2}$ | D. | 6+2$\sqrt{2}$ |
| 年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 支持 | a= | c= | |
| 不支持 | b= | d= | |
| 合计 |
参考数据:P(K2≥3.841)=0.050,P(k2≥6.635)=0.010,P(K2≥10.828)=0.001.
| A. | x2=4y | B. | x2=8y | C. | x2=6y | D. | x2=16y |
| 点击量 | [0,1000] | (1000,3000] | (3000,+∞) |
| 节数 | 6 | 18 | 12 |
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间[0,1000]内,则需要花费40分钟进行剪辑,若点击量在区间(1000,3000]内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间X的分布列与数学期望.