题目内容
9.为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄大点频数分布及支持“生育二胎”人数如下表:| 年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 支持 | a= | c= | |
| 不支持 | b= | d= | |
| 合计 |
参考数据:P(K2≥3.841)=0.050,P(k2≥6.635)=0.010,P(K2≥10.828)=0.001.
分析 (Ⅰ)根据题意填写2×2列联表,由表中数据计算观测值,对照临界值即可得出结论;
(Ⅱ)用列举法求出基本事件数,计算所求的概率值.
解答 解:(Ⅰ)根据题意填写2×2列联表如下;
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 支持 | a=3 | c=29 | 32 |
| 不支持 | b=7 | d=11 | 18 |
| 合 计 | 10 | 40 | 50 |
根据表中数据,计算${K^2}=\frac{{50×{{(3×11-7×29)}^2}}}{{({3+7})({29+11})({3+29})({7+11})}}≈6.27$<6.635;…(4分)
所以没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
…(5分)
(Ⅱ)年龄在[5,15)中支持“生育二胎”的4人分别为a,b,c,d,
不支持“生育二胎”的人记为M,…(6分)
则从年龄在[5,15)的被调查人中随机选取两人所有可能的结果有:
(a,b),(a,c),(a,d),(a,M),(b,c),(b,d),(b,M),
(c,d),(c,M),(d,M)共10种;…(8分)
设“恰好这两人都支持“生育二胎””为事件A,…(9分)
则事件A所有可能的结果有:
(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)共6种,
∴$P(A)=\frac{6}{10}=\frac{3}{5}$;…(11分)
所以对年龄在[5,15)的被调查人中随机选取两人进行调查时,
恰好这两人都支持“生育二胎”的概率为$\frac{3}{5}$.…(12分)
点评 本题考查了独立性检验与列举法求古典概型的概率问题,是基础题.

练习册系列答案
相关题目
19.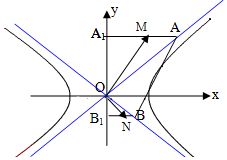 如图,A、B分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$两渐近线上的点,A、B在y轴上的射影分别为A1、B1,M、N分别是A1A、B1B、的中点,若AB中点在双曲线上,且$\overrightarrow{OM}•\overrightarrow{ON}≥-{a^2}$,则双曲线的离心率的取值范围为( )
如图,A、B分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$两渐近线上的点,A、B在y轴上的射影分别为A1、B1,M、N分别是A1A、B1B、的中点,若AB中点在双曲线上,且$\overrightarrow{OM}•\overrightarrow{ON}≥-{a^2}$,则双曲线的离心率的取值范围为( )
 如图,A、B分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$两渐近线上的点,A、B在y轴上的射影分别为A1、B1,M、N分别是A1A、B1B、的中点,若AB中点在双曲线上,且$\overrightarrow{OM}•\overrightarrow{ON}≥-{a^2}$,则双曲线的离心率的取值范围为( )
如图,A、B分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$两渐近线上的点,A、B在y轴上的射影分别为A1、B1,M、N分别是A1A、B1B、的中点,若AB中点在双曲线上,且$\overrightarrow{OM}•\overrightarrow{ON}≥-{a^2}$,则双曲线的离心率的取值范围为( )| A. | $({1,\frac{3}{2}}]$ | B. | $[\frac{3}{2},+∞)$ | C. | $(1,\frac{{\sqrt{5}}}{2}]$ | D. | $[\frac{{\sqrt{5}}}{2},+∞)$ |
20.在Rt△ABC中,两直角边分别为a,b,斜边为c,则由勾股定理知c2=b2+a2,则在四面体P-ABC中,PA⊥PB,PA⊥PC,PB⊥PC,类比勾股定理,类似的结论为( )
| A. | S△PBC2=S△PAB2+S△PAC2 | B. | S△ABC2=S△PAB2+S△PAC2 | ||
| C. | S△ABC2=S△PAB2+S△PAC2+S△PBC2 | D. | S△PBC2=S△PAB2+S△PAC2+S△ABC2 |
14.已知函数$f(x)=\frac{1-x}{{1+{x^2}}}{e^x}$,若f(x1)=f(x2),且x1<x2,关于下列命题:(1)f(x1)>f(-x2);(2)f(x2)>f(-x1);(3)f(x1)>f(-x1);(4)f(x2)>f(-x2).正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.已知正项等比数列{an}的前n项和为Sn,且S8-2S4=5,则a9+a10+a11+a12的最小值为( )
| A. | 10 | B. | 15 | C. | 20 | D. | 25 |
19.等比数列{an}中,a2,a6是方程x2-34x+64=0的两根,则a4等于( )
| A. | 8 | B. | -8 | C. | ±8 | D. | 以上都不对 |
