题目内容
4．已知点M在直线x+y+a=0上，过点M引圆x2+y2=2的切线，若切线长的最小值为2$\sqrt{2}$，则实数a的值为（ ）| A． | ±2$\sqrt{2}$ | B． | ±3 | C． | ±4 | D． | ±2$\sqrt{5}$ |
分析 根据题意画出图形，结合图形求出点O到直线x+y+a=0的距离d，利用勾股定理求出a的值．
解答 
解：设点O到直线x+y+a=0的距离为d，则d=$\frac{|a|}{\sqrt{2}}$；
又过点M引圆x2+y2=2的切线，
切线长的最小值为|MT|=2$\sqrt{2}$，
则r2+|MT|2=d2，
即2+${（2\sqrt{2}）}^{2}$=$\frac{{a}^{2}}{2}$，
解得a=±2$\sqrt{5}$．
故选：D．
点评 本题考查了直线与圆方程的应用问题，是基础题．
练习册系列答案
相关题目
19．
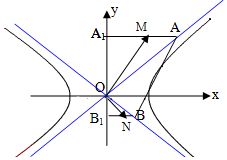如图，A、B分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$两渐近线上的点，A、B在y轴上的射影分别为A1、B1，M、N分别是A1A、B1B、的中点，若AB中点在双曲线上，且$\overrightarrow{OM}•\overrightarrow{ON}≥-{a^2}$，则双曲线的离心率的取值范围为（ ）
如图，A、B分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$两渐近线上的点，A、B在y轴上的射影分别为A1、B1，M、N分别是A1A、B1B、的中点，若AB中点在双曲线上，且$\overrightarrow{OM}•\overrightarrow{ON}≥-{a^2}$，则双曲线的离心率的取值范围为（ ）| A． | $（{1，\frac{3}{2}}]$ | B． | $[\frac{3}{2}，+∞）$ | C． | $（1，\frac{{\sqrt{5}}}{2}]$ | D． | $[\frac{{\sqrt{5}}}{2}，+∞）$ |
如图，平面PAC⊥平面ABC，点E、F、O分别为线段PA、PB、AC的中点，点G是线段CO的中点，AB=BC=AC=4，PA=PC=2$\sqrt{2}$．求证：
2017年5月，印度电影《摔跤吧！爸爸》在中国上映，为了了解银川观众的满意度，某影院随机调查了本市观看影片的观众，现从调查人群中随机抽取13名，并用如图所示的茎叶图记录了他们的满意度分数（10分制，且以小数点前的一位数字为茎，小数点后的一位数字为叶）．若分数不低于9分，则称该观众为“满意观众”．
在某单位的职工食堂中，食堂每天以3元/个的价格从面包店购进面包，然后以5元/个的价格出售．如果当天卖不完，剩下的面包以1元/个的价格卖给饲料加工厂．根据以往统计资料，得到食堂每天面包需求量的频率分布直方图如图所示．食堂某天购进了90个面包，以x（单位：个，60≤x≤110）表示面包的需求量，T（单位：元）表示利润．