题目内容
3.等差数列{an}中,2a1+3a2=11,2a3=a2+a6-4,其前n项和为Sn.(Ⅰ) 求数列{an}的通项公式;
(Ⅱ) 设数列{bn}满足bn=$\frac{1}{{S}_{n+1}-1}$,其前n项和为Tn,求证:Tn<$\frac{3}{4}$(n∈N*).
分析 (Ⅰ) 设等差数列{an}的公差为d,运用等差数列的通项公式,解方程可得首项和公差,即可得到所求;
(Ⅱ)运用等差数列的求和公式,求得Sn=n2,bn=$\frac{1}{{S}_{n+1}-1}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),由数列的求和方法:裂项相消求和,计算化简,再由不等式的性质,即可得证.
解答 解:(Ⅰ) 设等差数列{an}的公差为d,
因为2a1+3a2=11,2a3=a2+a6-4,
可得2a1+3(a1+d)=5a1+3d=11,2(a1+2d)=a1+d+a1+5d-4,
得d=2,a1=1,
所以an=a1+(n-1)d=1+2(n-1)=2n-1.
(Ⅱ)证明:Sn=na1+$\frac{1}{2}$n(n-1)d=n+$\frac{1}{2}$n(n-1)×2=n2,
bn=$\frac{1}{{S}_{n+1}-1}$=$\frac{1}{(n+1)^{2}-1}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
前n项和为Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{n-1}$-$\frac{1}{n+1}$+$\frac{1}{n}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$--$\frac{1}{n+1}$-$\frac{1}{n+2}$)=$\frac{3}{4}$-$\frac{3}{4}$($\frac{1}{n+1}$+$\frac{1}{n+2}$)<$\frac{3}{4}$.
即有Tn<$\frac{3}{4}$(n∈N*).
点评 本题考查等差数列通项公式和求和公式的运用,注意运用方程思想,考查数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案| A. | 对于线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,直线必经过点 $({\overline x,\overline y})$; | |
| B. | 茎叶图的优点在于它可以保存原始数据,并且可以随时记录; | |
| C. | 用秦九韶算法求多项式f(x)=3x5-2x3+6x2+x+1=2时的值时,v2=14; | |
| D. | 将一组数据中的每一个数据都加上或减去同一个常数后,方差恒不变. |
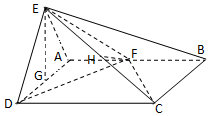 如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,P是O的中点,O是PQ的中点,EC与平面ABCD成30°角.
如图所示,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,P是O的中点,O是PQ的中点,EC与平面ABCD成30°角.