题目内容
已知函数y=f(x)是定义在(0,+∞)上的函数,对任意a,b∈(0,+∞)都有f(
)=f(a)-f(b),
(1)求证:f(ab)=f(a)+f(b);
(2)若当x>1时,f(x)>0,求证:函数y=f(x)在定义域上为增函数.
| a |
| b |
(1)求证:f(ab)=f(a)+f(b);
(2)若当x>1时,f(x)>0,求证:函数y=f(x)在定义域上为增函数.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)利用赋值法,分别令a=b=1,求得f(1)=0,再令b=
,问题得证.
(2)利用单调性的定义证明即可.
| 1 |
| b |
(2)利用单调性的定义证明即可.
解答:
证明(1):∵f(
)=f(a)-f(b),
令a=b=1,
则f(1)=f(1)-f(1),
∴f(1)=0
再令b=
,
∴f(ab)=f(a)-f(
)=f(a)-f(1)+f(b)=f(a)+f(b);
即问题得证.
(2)证明:∵对x1,x2∈(1,+∞),x1<x2,有
>1,
又x>1时,f(x)>0,
∴f(
)>0
∴f(x2)-f(x1)=f(
)>0
故函数y=f(x)在定义域上为增函数.
| a |
| b |
令a=b=1,
则f(1)=f(1)-f(1),
∴f(1)=0
再令b=
| 1 |
| b |
∴f(ab)=f(a)-f(
| 1 |
| b |
即问题得证.
(2)证明:∵对x1,x2∈(1,+∞),x1<x2,有
| x2 |
| x1 |
又x>1时,f(x)>0,
∴f(
| x2 |
| x1 |
∴f(x2)-f(x1)=f(
| x2 |
| x1 |
故函数y=f(x)在定义域上为增函数.
点评:本题考查的是抽象函数与函数的单调性知识的综合应用问题.在解答的过程当中充分体现了抽象函数特值的思想、函数单调性以及问题转化的思想.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
已知a,b∈R,下列四个条件中,使a<b成立的必要而不充分的条件是( )
| A、|a|<|b| |
| B、2a<2b |
| C、a<b-1 |
| D、a<b+1 |
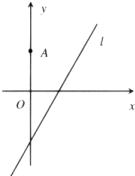 如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在直线l上.
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4,设圆C的半径为1,圆心在直线l上. 小华参加学校创意社团,上交一份如图所示的作品:边长为2的正方形中作一内切圆⊙O,在⊙O内作一个关于正方形对角线对称的内接“十”字形图案.OA垂直于该“十”字形图案的一条边,点P为该边上的一个端点.记“十”字形图案面积为S,∠AOP=θ.试用θ表示S,并由此求出S的最大值.
小华参加学校创意社团,上交一份如图所示的作品:边长为2的正方形中作一内切圆⊙O,在⊙O内作一个关于正方形对角线对称的内接“十”字形图案.OA垂直于该“十”字形图案的一条边,点P为该边上的一个端点.记“十”字形图案面积为S,∠AOP=θ.试用θ表示S,并由此求出S的最大值. 阅读如图所示算法:
阅读如图所示算法: