题目内容
13.对于曲线C:f(x,y)=0,若存在非负实数M和m,使得曲线C上任意一点P(x,y),m≤|OP|≤M恒成立(其中O为坐标原点),则称曲线C为有界曲线,且称M的最小值M0为曲线C的外确界,m的最大值m0为曲线C的内确界.(1)写出曲线x+y=1(0<x<4)的外确界M0与内确界m0;
(2)曲线y2=4x与曲线(x-1)2+y2=4是否为有界曲线?若是,求出其外确界与内确界;若不是,请说明理由;
(3)已知曲线C上任意一点P(x,y)到定点F1(-1,0),F2(1,0)的距离之积为常数a(a>0),求曲线C的外确界与内确界.
分析 (1)由外确界与内确界的概念,结合曲线方程,即可求出答案.
(2)由外确界与内确界的概念,结合曲线方程,即可求出答案.
(2)由题意求出曲线C的方程,进一步得到x的范围,把x2+y2转化为含有x的代数式,分类讨论得答案.
解答 解.(1)曲线x+y=1(0<x<4)的外确界M0=5与内确界${m_0}=\frac{{\sqrt{2}}}{2}$.
(2)对于曲线y2=4x,设P(x,y)为曲线上任意一点$|OP|=\sqrt{{x^2}+{y^2}}=\sqrt{{x^2}+4x}=\sqrt{{{(x+2)}^2}-4}(x≥0)$,
∴|OP|∈[0,+∞),
∴曲线y2=4x不是有界曲线.
对于曲线(x-1)2+y2=4$|OP|=\sqrt{{x^2}+{y^2}}=\sqrt{{x^2}+4-{{(x-1)}^2}}=\sqrt{2x+3}(-1≤x≤3)$,
∴|OP|∈[1,3],
∴曲线(x-1)2+y2=4是有界曲线,外确界M0=3与内确界m0=1.
(3)由已知得:$\sqrt{{{(x-1)}^2}+{y^2}}×\sqrt{{{(x+1)}^2}+{y^2}}=a$$\sqrt{{x^2}-2x+1+{y^2}}×\sqrt{{x^2}+2x+1+{y^2}}=\sqrt{{{({x^2}+{y^2}+1)}^2}-4{x^2}}=a$,
∴(x2+y2+1)2-4x2=a2,
∴${y^2}=\sqrt{4{x^2}+{a^2}}-({x^2}+1)$,
∵y2≥0,
∴$\sqrt{4{x^2}+{a^2}}≥{x^2}+1$,
∴(x2+1)2≤4x2+a2,
∴(x2-1)2≤a2,
∴1-a≤x2≤a+1,
∵$|OP|=\sqrt{{x^2}+{y^2}}=\sqrt{\sqrt{4{x^2}+{a^2}}-1}$
若0<a<1,则$\sqrt{1-a}≤\sqrt{\sqrt{4{x^2}+{a^2}}-1}≤\sqrt{a+1}$,外确界${M_0}=\sqrt{a+1}$,内确界${m_0}=\sqrt{1-a}$
若a≥1,0≤x2≤a+1,则$\sqrt{a-1}≤\sqrt{\sqrt{4{x^2}+{a^2}}-1}≤\sqrt{a+1}$,外确界${M_0}=\sqrt{a+1}$,内确界${m_0}=\sqrt{a-1}$
综合得:外确界${M_0}=\sqrt{a+1}$,内确界${m_0}=\sqrt{|a-1|}$.
点评 本题考查曲线的外确界与内确界的求法,体现了分类讨论的数学思想方法,理解题意是关键,注意函数与方程思想的合理运用,属难题.

| A. | 1 | B. | 2 | C. | -3 | D. | -4 |
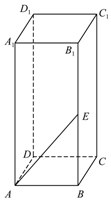 如图所示,长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.过点A1,D1,E的平面α与此长方体的面相交,交线围成一个四边形.
如图所示,长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.过点A1,D1,E的平面α与此长方体的面相交,交线围成一个四边形.