题目内容
2.曲线y=ex+1在点(0,2)处的切线与直线y=0和x=0围成的三角形面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
分析 求出导数,求得切线的斜率,由点斜式方程可得切线的方程,求得与x轴、y轴的交点,由三角形的面积公式可得所求值.
解答 解:y=ex+1的导数为y′=ex,
可得曲线y=ex+1在点(0,2)处的切线斜率为k=1,
可得切线方程为y=x+2,
即有与坐标轴的交点为(-2,0)和(0,2),
所以与坐标轴围成的三角形的面积为$S=\frac{1}{2}×2×2=2$,
故选:D.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义,正确求导是解题的关键,属于基础题.

练习册系列答案
相关题目
12.已知点(2,1)在双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线上,则C的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | $\frac{\sqrt{5}}{2}$ |
7.下列四个式子中是恒等式的是( )
| A. | sin(α+β)=sinα+sinβ | B. | cos(α+β)=cosαcosβ+sinβsinβ | ||
| C. | tan(α+β)=$\frac{tanα-tanβ}{1-tanαtanβ}$ | D. | sin(α+β)sin(α-β)=sin2α-sin2β |
11.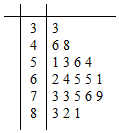 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,并估计用户对该公司的产品“满意”的概率;
(Ⅱ) 根据列联表数据判断:能否在犯错的概率不超过5%的前提下,认为“满意与否”与“性别”有关?
附:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$其中n=a+b+c+d
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,(Ⅰ)根据以上资料完成下面的2×2列联表,并估计用户对该公司的产品“满意”的概率;
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
附:
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
12.已知具有线性相关的两个变量x,y之间的一组数据如表:
且回归方程是$\stackrel{∧}{y}$=0.95x+2.6,则t=( )
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2.2 | 4.3 | t | 4.8 | 6.7 |
| A. | 2.5 | B. | 3.5 | C. | 4.5 | D. | 5.5 |
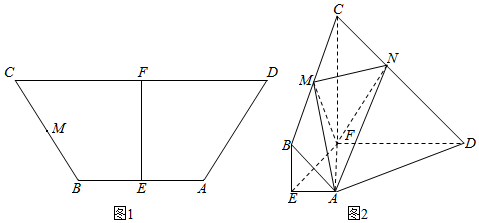
 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°. 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知:∠ABC=45°,AB=2,$BC=2\sqrt{2}$,SB=SC,直线SA与平面ABCD所成角为45°,O为BC的中点.
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知:∠ABC=45°,AB=2,$BC=2\sqrt{2}$,SB=SC,直线SA与平面ABCD所成角为45°,O为BC的中点.