题目内容
12.已知点(2,1)在双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线上,则C的离心率为( )| A. | $\sqrt{5}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | $\frac{\sqrt{5}}{2}$ |
分析 求出双曲线的渐近线方程,由题意可得a=2b,运用双曲线的离心率公式计算即可得到所求值.
解答 解:双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线方程为y=±$\frac{b}{a}$x,
由题意可得$\frac{2b}{a}$=1,即a=2b,
c=$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{\sqrt{5}}{2}$a,可得e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$.
故选:D.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的渐近线方程,考查离心率公式的运用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若α∈($\frac{π}{4}$,$\frac{π}{2}$),则sinα,cosα,tanα的大小关系是( )
| A. | sinα>cosα>tanα | B. | tanα>cosα>sinα | C. | cosα>tanα>sinα | D. | tanα>sinα>cosα |
7.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与直线y=x交于不同的两点,则双曲线C的离心率的取值范围是( )
| A. | (1,$\sqrt{2}$)∪($\sqrt{2}$,+∞) | B. | ($\sqrt{2}$,+∞) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
2.曲线y=ex+1在点(0,2)处的切线与直线y=0和x=0围成的三角形面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
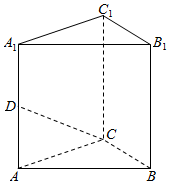 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,BC=1,$∠BAC=\frac{π}{6}$,D为棱AA1中点,证明异面直线B1C1与CD所成角为$\frac{π}{2}$,并求三棱柱ABC-A1B1C1的体积.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,BC=1,$∠BAC=\frac{π}{6}$,D为棱AA1中点,证明异面直线B1C1与CD所成角为$\frac{π}{2}$,并求三棱柱ABC-A1B1C1的体积. 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3D为AC的中点
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3D为AC的中点