题目内容
12.以直角坐标系原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为$\left\{\begin{array}{l}x=\frac{1}{2}+tcosα\\ y=tsinα\end{array}$,(t为参数,0<α<π),曲线C的极坐标方程ρ=$\frac{2cosθ}{si{n}^{2}θ}$.(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A,B两点,当α=$\frac{π}{3}$,求|AB|的值.
分析 (1)利用互化公式即可得出直角坐标方程.
(2)将直线l的参数方程代入y2=2x,得t2sin2α-2tcos α-1=0,设A,B两点对应的参数分别为t1,t2,利用根与系数的关系、弦长公式即可得出.
解答 解:(1)由ρ=$\frac{2cosθ}{si{n}^{2}θ}$,得ρ2sin2θ=2ρcos θ,所以曲线C的直角坐标方程为y2=2x.
(2)将直线l的参数方程代入y2=2x,得t2sin2α-2tcos α-1=0,
设A,B两点对应的参数分别为t1,t2,
则t1+t2=$\frac{2cosα}{si{n}^{2}α}$,t1•t2=-$\frac{1}{sin2α}$,
所以|AB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{\frac{4co{s}^{2}α}{si{n}^{4}α}+\frac{4}{si{n}^{2}α}}$=$\frac{2}{si{n}^{2}α}$=$\frac{8}{3}$.
点评 本题考查了极坐标方程化为直角坐标方程、一元二次方程的根与系数的关系、弦长公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
3.在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如表:
(1)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(2)用上表数据画出散点图易发现历史成绩y与语文成绩x具有较强的线性相关关系,求y与x的线性回归方程(系数精确到0.1).参考公式:回归直线方程是y=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$.
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 语文成绩x | 60 | 70 | 74 | 90 | 94 | 110 |
| 历史成绩y | 58 | 63 | 75 | 79 | 81 | 88 |
(2)用上表数据画出散点图易发现历史成绩y与语文成绩x具有较强的线性相关关系,求y与x的线性回归方程(系数精确到0.1).参考公式:回归直线方程是y=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$.
7.已知集合A={0,1,2},A∩B={0,2},则B集合可能是( )
| A. | {0,1} | B. | {1,2} | C. | {0,2,3} | D. | {0} |
1.若集合A={-2,-1,0,1,2},集合B={x|x(x+3)<0},则A∩B等于( )
| A. | {-1,0,1,2} | B. | {-2,-1} | C. | {1,2} | D. | {0,1,2} |
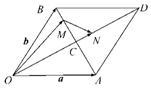 如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,试用a,b表示$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{MN}$.
如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,试用a,b表示$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{MN}$.