题目内容
20.△ABC中,角A、B、C的对边分别为a、b、c,a=2,C=$\frac{π}{3}$.(1)若$A=\frac{π}{4}$,求c;
(2)若△ABC的面积$S=\sqrt{3}$,求b,c.
分析 (1)利用正弦定理直接求解即可.
(2)利用三角形的面积公式求出b,然后求解c即可.
解答 解:(1)由 $\frac{a}{sinA}=\frac{c}{sinC}$,得$c=\frac{asinC}{sinA}=\frac{{2×\frac{{\sqrt{3}}}{2}}}{{\frac{{\sqrt{2}}}{2}}}=\sqrt{6}$.
(2)$S=\frac{1}{2}absinC$,即$\frac{1}{2}×2b×\frac{{\sqrt{3}}}{2}=\sqrt{3}$,得b=2
又a=2,$C=\frac{π}{3}$,故△ABC为等边三角形,所以c=2.
点评 本题考查正弦定理的应用,三角形的边长的求解,考查计算能力.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
11.下列结论正确的是( )
| A. | 若ac>bc,则a>b | B. | 若a2>b2,则a>b | ||
| C. | 若a>b,c<0,则a+c<b+c | D. | 若$\sqrt{a}$<$\sqrt{b}$,则a<b |
8.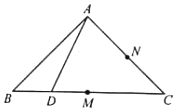 在等腰直角△ABC中,AB⊥AC,BC=2,M为BC中点,N为AC中点,D为BC边上一个动点,△ABD沿AD翻折使BD⊥DC,点A在面BCD上的投影为点O,当点D在BC上运动时,以下说法错误的是( )
在等腰直角△ABC中,AB⊥AC,BC=2,M为BC中点,N为AC中点,D为BC边上一个动点,△ABD沿AD翻折使BD⊥DC,点A在面BCD上的投影为点O,当点D在BC上运动时,以下说法错误的是( )
 在等腰直角△ABC中,AB⊥AC,BC=2,M为BC中点,N为AC中点,D为BC边上一个动点,△ABD沿AD翻折使BD⊥DC,点A在面BCD上的投影为点O,当点D在BC上运动时,以下说法错误的是( )
在等腰直角△ABC中,AB⊥AC,BC=2,M为BC中点,N为AC中点,D为BC边上一个动点,△ABD沿AD翻折使BD⊥DC,点A在面BCD上的投影为点O,当点D在BC上运动时,以下说法错误的是( )| A. | 线段NO为定长 | B. | $|CO|∈[1,\sqrt{2})$ | C. | ∠AMO+∠ADB>180° | D. | 点O的轨迹是圆弧 |
15.在△ABC中,$\overrightarrow{AB}=\overrightarrow c$,$\overrightarrow{AC}=\overrightarrow b$.若点D满足$\overrightarrow{CD}=2\overrightarrow{DB}$,则$\overrightarrow{AD}$=( )
| A. | $\frac{2}{3}\overrightarrow b+\frac{1}{3}\overrightarrow c$ | B. | $\frac{1}{3}\overrightarrow b+\frac{2}{3}\overrightarrow c$ | C. | $\frac{2}{3}$$\overrightarrow{b}$-$\frac{1}{3}$$\overrightarrow{c}$ | D. | $\frac{1}{3}\overrightarrow b-\frac{2}{3}\overrightarrow c$ |
9.等差数列{an}共有2n+1项,其中奇数项之和为319,偶数项之和为290,则其中间项为( )
| A. | 28 | B. | 29 | C. | 30 | D. | 31 |
4.如图所示,在?ABCD中,AE:EB=1:2,若S△AEF=6cm2,则S△CDF为( )
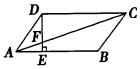

| A. | 54cm2 | B. | 24cm2 | C. | 18cm2 | D. | 12cm2 |
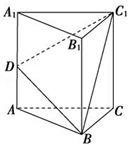 如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=$\sqrt{3}$,则球O的体积等于$\frac{9π}{2}$.
如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=$\sqrt{3}$,则球O的体积等于$\frac{9π}{2}$.