��Ŀ����
17����֪{ an }��һ���������0�ĵȲ����У�������a3a6=55��a2+a7=16����1��������{ an }��ͨ�ʽ��
��2��������{bn}����$\frac{{b}_{1}}{2}+\frac{{b}_{2}}{{2}^{2}}+\frac{{b}_{3}}{{2}^{3}}$+��+$\frac{{b}_{n}}{{2}^{n}}$=an ��n��N* �� ������{bn}��ǰn���Sn��
���� ��1������֪��ʽ��õȲ����еĹ������Ȳ����е�ͨ�ʽ�������{ an }��ͨ�ʽ��
��2����$\frac{{b}_{1}}{2}+\frac{{b}_{2}}{{2}^{2}}+\frac{{b}_{3}}{{2}^{3}}$+��+$\frac{{b}_{n}}{{2}^{n}}$=an ���b1��bn���ɵ�����{bn}����2Ϊ�����2Ϊ���ȵĵȱ����У�������{bn}��ǰn���Sn����
��� �⣺��1��������{ an }�ǵȲ����У���a2+a7=16��
��a3+a6=16���֡�a3a6=55��������{ an }�Ĺ������0��
��a3=5��a6=11�����乫��d=$\frac{{a}_{6}-{a}_{3}}{6-3}=\frac{11-5}{3}$=2��
��an=a3+��n-3��•2=5+2n-6=2n-1��
��2���������b1=2a1=2��
��n��2ʱ��an-an-1=��$\frac{{b}_{1}}{2}+\frac{{b}_{2}}{{2}^{2}}+\frac{{b}_{3}}{{2}^{3}}$+��+$\frac{{b}_{n}}{{2}^{n}}$��-��$\frac{{b}_{1}}{2}+\frac{{b}_{2}}{{2}^{2}}+\frac{{b}_{3}}{{2}^{3}}$+��+$\frac{{b}_{n-1}}{{2}^{n-1}}$��
=$\frac{{b}_{n}}{{2}^{n}}=��2n-1��-[2��n-1��-1]=2$��
��${b}_{n}={2}^{n+1}$����$\frac{{b}_{n+1}}{{b}_{n}}=\frac{{2}^{n+1}}{{2}^{n+1}}=2$��
������{bn}����2Ϊ�����2Ϊ���ȵĵȱ����У���ǰn���Sn=$\frac{2��1-{2}^{n}��}{1-2}={2}^{n+1}-2$��
���� ���⿼�����е���ʽ�������˵Ȳ����е����ʺ͵ȱȹ�ϵ��ȷ����ѵ���˵ȱ�����ǰn��͵������е��⣮

 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�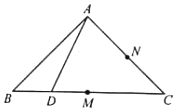 �ڵ���ֱ�ǡ�ABC�У�AB��AC��BC=2��MΪBC�е㣬NΪAC�е㣬DΪBC����һ�����㣬��ABD��AD����ʹBD��DC����A����BCD�ϵ�ͶӰΪ��O������D��BC���˶�ʱ������˵��������ǣ�������
�ڵ���ֱ�ǡ�ABC�У�AB��AC��BC=2��MΪBC�е㣬NΪAC�е㣬DΪBC����һ�����㣬��ABD��AD����ʹBD��DC����A����BCD�ϵ�ͶӰΪ��O������D��BC���˶�ʱ������˵��������ǣ�������| A�� | �߶�NOΪ���� | B�� | $|CO|��[1��\sqrt{2}��$ | C�� | ��AMO+��ADB��180�� | D�� | ��O�Ĺ켣��Բ�� |
| A�� | 28 | B�� | 29 | C�� | 30 | D�� | 31 |
| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 90�� |
 �۲���ͼ��ʾ��������ͼ����ÿ���ߣ����������˵㣩��n��n��2��n��N*����Բ�㣬��n��ͼ����Բ���������Sn�����˹����ƶϳ�Sn��n�Ĺ�ϵʽΪ��������
�۲���ͼ��ʾ��������ͼ����ÿ���ߣ����������˵㣩��n��n��2��n��N*����Բ�㣬��n��ͼ����Բ���������Sn�����˹����ƶϳ�Sn��n�Ĺ�ϵʽΪ��������| A�� | Sn=2n | B�� | Sn=4n | C�� | Sn=2n | D�� | Sn=4n-4 |
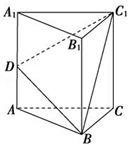 ��ͼ����֪��O�������ĵ�A��B��C��D��DA��ƽ��ABC��AB��BC��DA=AB=BC=$\sqrt{3}$������O���������$\frac{9��}{2}$��
��ͼ����֪��O�������ĵ�A��B��C��D��DA��ƽ��ABC��AB��BC��DA=AB=BC=$\sqrt{3}$������O���������$\frac{9��}{2}$��