题目内容
18.若函数f(x)=lnx-$\frac{1}{2}$ax2-2x存在递减区间,则实数a的最小整数值是0.分析 首先分析求出函数的定义域,对f(x)求导可得$f′(x)=\frac{1}{x}-ax-2$,根据题意,有f′(x)<0,变形可得$a>\frac{1-2x}{{x}^{2}}$,结合x的范围,可得a>-1,即可得答案.
解答 由题意,x>0,$f′(x)=\frac{1}{x}-ax-2$,
已知函数存在单调递减区间,由f′(x)<0有解,即$a>\frac{1-2x}{{x}^{2}}$有解,
令$y=\frac{1-2x}{{x}^{2}}$,$y′=-\frac{2(1-x)}{{x}^{3}}(x>0)$,
故y=$\frac{1-2x}{{x}^{2}}$在(0,1)上递减,在(1,+∞)上递增,
则有${y}_{min}=\frac{1-2×1}{{1}^{2}}=-1$,
∴a>-1,(经检验a=-1时f(x)不存在单调区间).
即实数a的最小整数值为0
点评 本题考查函数的单调性与其导数的关系,解题时注意要先分析函数的定义域,解题过程中注意对“存在”这类问题的理解,学生在处理时往往容易出错.

练习册系列答案
相关题目
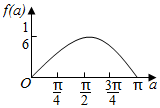
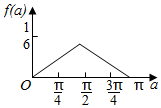
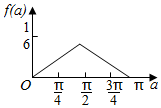
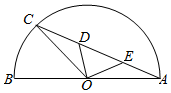 如图,$\widehat{AB}$为半圆,O为圆心,OA=1,C为$\widehat{AB}$上的动点,D、E为线段AC的三等分点,设∠AOC=α,将△ODE的面积为y=f(α),则y=f(α)的图象大致为( )
如图,$\widehat{AB}$为半圆,O为圆心,OA=1,C为$\widehat{AB}$上的动点,D、E为线段AC的三等分点,设∠AOC=α,将△ODE的面积为y=f(α),则y=f(α)的图象大致为( )