题目内容
（本小题满分12分）证明：
能够被6整除.
能够被6整除.见解析.
本试题主要是考查了运用数学归纳法证明与自然数有关的命题的证明问题的运用。首先对于n=1证明，然后假设当当
时，命题成立，即
能够被6整除.，在此基础上可推导当
时，命题也成立即可。
证明：1）当
时，
显然能够被6整除，命题成立.
2）假设当时，命题成立，即能够被6整除.
当时，
.
由假设知能够被6整除，而
是偶数，故
能够被6整除，从而
即
能够被6整除.因此，当时命题成立.
由1）2）知，命题对一切正整数成立，即能够被6整除;
时，命题成立，即能够被6整除.，在此基础上可推导当时，命题也成立即可。证明：1）当
时，显然能够被6整除，命题成立.2）假设当
时，命题成立，即能够被6整除.当
时，.由假设知
能够被6整除，而是偶数，故能够被6整除，从而即能够被6整除.因此，当时命题成立.由1）2）知，命题对一切正整数成立，即
能够被6整除;
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
，
（
、
）。
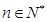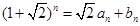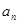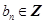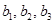的值；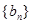
的各项均为奇数.
（
）
，第二步由k到k+1时不等式左边需增加（ ）
,在验证
成立时,左边所得的项为 ( )
+
+
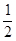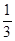时，在第二步证明从n=k到n=k+1成立时，左边增加的项数是（ ）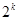
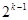
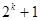
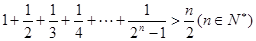时，假设当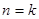
时成立，则当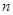
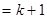时，左边增加的项数为（ ）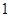
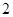
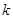
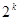
， (a≠1，n∈N)”时，在验证n=1成立时，左边应该是 （ ）