��Ŀ����
19�� ��ͼ����֪������y=x2+4x+3�Ķ���ΪA����������x���ཻ�ڵ�B�͵�C����B�ڵ�C����ࣩ����y���ཻ�ڵ�D����PΪ�Գ���ֱ��l�ϵ�һ�����㣬��ÿ��1����λ���ȵ��ٶȴ������ߵĶ���A�����˶������P�˶���ʱ��Ϊt�룮
��ͼ����֪������y=x2+4x+3�Ķ���ΪA����������x���ཻ�ڵ�B�͵�C����B�ڵ�C����ࣩ����y���ཻ�ڵ�D����PΪ�Գ���ֱ��l�ϵ�һ�����㣬��ÿ��1����λ���ȵ��ٶȴ������ߵĶ���A�����˶������P�˶���ʱ��Ϊt�룮��1�����C�����ꣻ
��2���ٵ�tΪ2��ʱ����PCD���ܳ���С��
�ڵ�tΪ4��$\sqrt{6}$��4��ʱ����PCD����CDΪ���ĵ��������Σ�������������ţ�
��3��̽����P���˶������У��Ƿ����һ��P��ʹ��PCD����CDΪб�ߵ�ֱ�������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���� ��1����y=0�����x=-3��-1�����ɵõ�C�����ꣻ
��2��������CDΪ��ֵ��ֻ��PC+PD�ĺ���С����CΪB����ֱ��x=-2�Գƣ�����BD�����ɵõ���Сֵ�ĵ�P����������ɵ�PD=CD��PC=CD����������ľ��빫ʽ���㼴�ɵõ�����
��3����3���������һ��P��ʹ��PCD����CDΪб�ߵ�ֱ�������Σ���P��-2��n��������PC��PD��������ֱ�ߴ�ֱ��������б��֮��Ϊ-1�����㼴�ɵõ�����ֵ��
��� 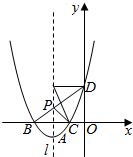 �⣺��1��������y=x2+4x+3����y=0���ɵ�x=-3��-1��
�⣺��1��������y=x2+4x+3����y=0���ɵ�x=-3��-1��
����C��-1��0����
��2������y=0�ɵ�B��-3��0����C��-1��0����
��x=0���ɵ�y=3����D��0��3����
����CDΪ��ֵ��ֻ��PC+PD�ĺ���С��
��CΪB����ֱ��x=-2�Գƣ�����BD��
����PC+PD����СֵΪBD��
��BD�ķ���Ϊy=x+3����x=-2�����y=1��
����P��-2��1����
��A��-2��-1�����ɵ�t=2��ʱ�ܳ���С��
��������ɵ�PD=CD��PC=CD��
��P��-2��m��������$\sqrt{4+��m-3��^{2}}$=$\sqrt{10}$��$\sqrt{1+{m}^{2}}$=$\sqrt{10}$��
���m=3��$\sqrt{6}$��m=3��-3��ȥ����
����t=4��$\sqrt{6}$��4��
��3���������һ��P��ʹ��PCD����CDΪб�ߵ�ֱ�������Σ�
��P��-2��n��������PC��PD��
�ɵ�kPC•kPD=-1����Ϊ$\frac{n}{-1}$•$\frac{n-3}{-2}$=-1��
���n=1��2��
�ʴ���һ��P��-2��1����-2��2����
ʹ��PCD����CDΪб�ߵ�ֱ�������Σ�
�ʴ�Ϊ��2��4��$\sqrt{6}$��4��
���� ���⿼����κ�����ͼ������ʣ����������ε���״���жϺ����ã�ע�����öԳ�������Сֵ���Լ�ֱ�ߴ�ֱ���������������������������е��⣮

| A�� | $\frac{\sqrt{6}}{2}$ | B�� | $\frac{\sqrt{6}}{3}$ | C�� | $\frac{\sqrt{6}}{4}$ | D�� | $\sqrt{2}$ |
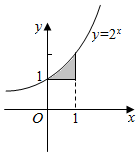
| A�� | ${��}_{0}^{1}$2xdx | B�� | ${��}_{0}^{1}$��2x-1��dx | C�� | ${��}_{0}^{1}$��2x+1��dx | D�� | ${��}_{0}^{1}$��1-2x��dx |
| A�� | 1 | B�� | 2 | C�� | $\frac{5}{2}$ | D�� | $\frac{7}{2}$ |
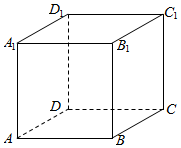 ��ͼ��ʾ�����ⳤΪ1��������ABCD-A1B1C1D1�У�
��ͼ��ʾ�����ⳤΪ1��������ABCD-A1B1C1D1�У�