题目内容
4.已知θ满足$\left\{\begin{array}{l}{a\frac{1}{co{s}^{2}θ}-bcosθ=2a}\\{bco{s}^{2}θ-a\frac{1}{cosθ}=2b}\end{array}\right.$ (a,b≠0),那么a、b的关系为a±b=0.分析 分别变形两式为$\frac{b}{a}$的形式,解cosθ可得.
解答 解:由第一式可得a($\frac{1}{co{s}^{2}θ}$-2)=bcosθ,
整理可得$\frac{b}{a}$=$\frac{1-2co{s}^{2}θ}{co{s}^{3}θ}$,
由第二式可得b(cos2θ-2)=a$\frac{1}{cosθ}$,
整理可得$\frac{b}{a}$=$\frac{1}{cosθ(co{s}^{2}θ-2)}$,
∴$\frac{1-2co{s}^{2}θ}{co{s}^{3}θ}$=$\frac{1}{cosθ(co{s}^{2}θ-2)}$,
解得cosθ=±1,∴$\frac{b}{a}$=±1,∴a±b=0
故答案为:a±b=0
点评 本题考查三角函数恒等变换,涉及三角函数公式和解方程组的思想,属基础题.

练习册系列答案
相关题目
15.数列{an}满足an-an+1=anan+1(n∈N*),数列{bn}满足bn=$\frac{1}{{a}_{n}}$,且b1+b2+…+b9=90,则b4•b6( )
| A. | 最大值为99 | B. | 为定值99 | C. | 最大值为100 | D. | 最大值为200 |
 如图,已知抛物线y=x2+4x+3的顶点为A,抛物线与x轴相交于点B和点C(点B在点C的左侧),与y轴相交于点D,点P为对称轴直线l上的一个动点,以每秒1个单位长度的速度从抛物线的顶点A向上运动,设点P运动的时间为t秒.
如图,已知抛物线y=x2+4x+3的顶点为A,抛物线与x轴相交于点B和点C(点B在点C的左侧),与y轴相交于点D,点P为对称轴直线l上的一个动点,以每秒1个单位长度的速度从抛物线的顶点A向上运动,设点P运动的时间为t秒.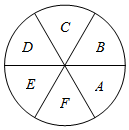 如图所示,6个扇形区域A,B,C,D,E,F,现给这6个区域着色,要求同一个区域涂同一种颜色,相邻的两个区城不得使用同一种颜色,现有4种不同的颜色可用,那么一共有多少种不同的涂色方法?
如图所示,6个扇形区域A,B,C,D,E,F,现给这6个区域着色,要求同一个区域涂同一种颜色,相邻的两个区城不得使用同一种颜色,现有4种不同的颜色可用,那么一共有多少种不同的涂色方法?