Question

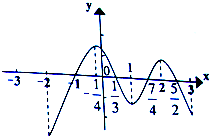函数y=f（x）在定义域（-2，3）内可导，其图象如图所示，记y=f（x）的导函数为y=f′（x），则不等式f′（x）≤0的解集为（　　）

• A、[-1，

  1

  3

  ]∪[

  7

  4

  ，

  5

  2

  ]
• B、[-

  1

  4

  ，1]∪[2，3]
• C、（-2，-

  1

  4

  ]∪[1，2]
• D、（-2，-1]∪[

  1

  3

  ，

  7

  4

  ]∪[

  5

  2

  ，3）

Answer 1

考点：利用导数研究函数的单调性

专题：导数的综合应用

分析：由函数图象求得函数在定义域（-2，3）内的减区间，根据导数大于0时函数单调递增，导数小于0时原函数单调递减确定不等式f′（x）≤0的解集．

解答： 解：由原函数图象可知，函数的减区间为：[-

1

4

，1]∪[2，3]．
根据导数小于0时原函数单调递减，可知不等式f′（x）≤0的解集为：[-

1

4

，1]∪[2，3]．
故选：B．

点评：本题主要考查了函数的单调性与导数的关系，解题的关键是识图，是中档题．