题目内容
已知等差数列{an}的前n项和为Sn,且满足a5+a9=24,a3:a11=1:2,则
等于( )
| lim |
| n→∞ |
| nan |
| S2n |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
考点:极限及其运算,等差数列的性质
专题:计算题,等差数列与等比数列
分析:先求出数列的首项与公差,可得数列的通项与S2n,即可求极限.
解答:
解:∵a5+a9=24,a3:a11=1:2,
∴a3+a11=24,a3:a11=1:2,
∴a3=8,a11=16,
∴d=1,a1=6,
∴an=n+5,S2n=
=n(2n+11),
∴
=
=
.
故选:D.
∴a3+a11=24,a3:a11=1:2,
∴a3=8,a11=16,
∴d=1,a1=6,
∴an=n+5,S2n=
| 2n(6+2n+5) |
| 2 |
∴
| lim |
| n→∞ |
| nan |
| S2n |
| lim |
| n→∞ |
| n(n+5) |
| n(2n+11) |
| 1 |
| 2 |
故选:D.
点评:本题考查等差数列的通项公式和前n项和公式,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知函数y=
,y=3x-5,y=lg(x2-4x+3)的定义域分别是P、Q、M,则它们之间的关系是( )
| 1 | ||
|
| A、P?Q?M |
| B、P?M?Q |
| C、Q?M?P |
| D、M?P?Q |
给出下列四个命题,其中真命题是( )
| A、?x∈R,x2>0 |
| B、?x∈Z,x3<1 |
| C、?x∈N*,x>1 |
| D、?x∈Q,x2=2 |
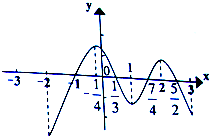 函数y=f(x)在定义域(-2,3)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域(-2,3)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )A、[-1,
| ||||||
B、[-
| ||||||
C、(-2,-
| ||||||
D、(-2,-1]∪[
|
对任意实数x,y,定义运算x*y=ax+by+cxy,其中a,b,c是常数,等式右边的运算是通常的加法和乘法运算.已知1*2=3,2*3=4,并且有一个非零常数m,使得对任意实数x,都有x*m=x,则m的值是( )
| A、-5 | B、-4 | C、4 | D、6 |
要得到函数y=2sin(2x-
)的图象,只需要将函数y=2sin2x的图象向( )平移( )个单位.括号中应填入( )
| π |
| 2 |
A、左
| ||
B、右
| ||
C、左
| ||
D、右
|
