题目内容
已知
+
=1（x＞0，y＞0），则xy的最小值（ ）
| 5 |
| x |
| 3 |
| y |
| A、15 | B、6 | C、60 | D、1 |
考点：基本不等式
专题：不等式的解法及应用
分析：利用基本不等式的性质即可得出．
解答：
解：∵x＞0，y＞0，
∴1=
+
≥2
，化为xy≥60，当且仅当y=6，x=10时取等号．
∴xy的最小值为60．
故选：C．
∴1=
| 5 |
| x |
| 3 |
| y |
|
∴xy的最小值为60．
故选：C．
点评：本题考查了基本不等式的性质，属于基础题．
练习册系列答案
相关题目
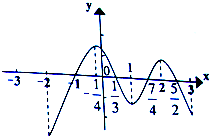函数y=f（x）在定义域（-2，3）内可导，其图象如图所示，记y=f（x）的导函数为y=f′（x），则不等式f′（x）≤0的解集为（ ）A、[-1，
| ||||||
B、[-
| ||||||
C、（-2，-
| ||||||
D、（-2，-1]∪[
|
若圆x2+y2-2x=0的圆心到直线x-y+a=0的距离为
，则a的值为（ ）
| ||
| 2 |
| A、0 | B、-2 |
| C、2或0 | D、0或-2 |
要得到函数y=2sin（2x-
）的图象，只需要将函数y=2sin2x的图象向（ ）平移（ ）个单位．括号中应填入（ ）
| π |
| 2 |
A、左
| ||
B、右
| ||
C、左
| ||
D、右
|
执行如图的程序框图，若输入n的值是100，则输出的变量是S与T的差是（ ）
| A、-50 | B、50 | C、0 | D、10 |
已知f（x）是定义在R上的奇函数，且当x≥0时，f（x）=x2，对任意的x∈[t，t+2]不等式f（x+t）≥2f（x）恒成立，那么实数t的取值范围是（ ）
A、[
| ||
| B、[2，+∞） | ||
C、（0，
| ||
D、[0，
|
若sin（α+
）=
，则cos2α=（ ）
| π |
| 2 |
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
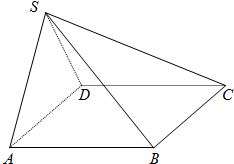如图，在四棱锥S-ABCD中，底面ABCD是边长为a的正方形，侧面SAD为正三角形，且垂直于底面ABCD．