题目内容
已知全集U=R,A={x|y=
},B={y|y=2x,x>0},则图中阴影部分所表示的集合是( )
| 2x-x2 |

| A、[0,2] |
| B、[0,1] |
| C、[0,1)∪(2,+∞) |
| D、[0,1]∪(2,+∞) |
考点:Venn图表达集合的关系及运算
专题:集合
分析:阴影部分表示的集合为(A∪B)∩(∁U(A∩B)),然后根据集合的基本运算,即可得到结论.
解答:
解:阴影部分表示的集合为(A∪B)∩(∁U(A∩B)),
∵A={x|y=
}={x|2x-x2≥0}={x|0≤x≤2},B={y|y=2x,x>0}={y|y>1},
∴A∪B={x|x≥0},A∩B={x|1<x≤2},
(∁U(A∩B)={x|x>2或x≤1,
则(A∪B)∩(∁U(A∩B))={x|0≤x≤1或x>2}=[0,1]∪(2,+∞).
故选:D.
∵A={x|y=
| 2x-x2 |
∴A∪B={x|x≥0},A∩B={x|1<x≤2},
(∁U(A∩B)={x|x>2或x≤1,
则(A∪B)∩(∁U(A∩B))={x|0≤x≤1或x>2}=[0,1]∪(2,+∞).
故选:D.
点评:本题主要考查集合的基本运算,利用Venn图确定集合的关系是解决本题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知函数y=
,y=3x-5,y=lg(x2-4x+3)的定义域分别是P、Q、M,则它们之间的关系是( )
| 1 | ||
|
| A、P?Q?M |
| B、P?M?Q |
| C、Q?M?P |
| D、M?P?Q |
已知函数f(x)=(
)x-log2x,若x0是函数y=f(x)的零点,且0<x1<x0,则有( )
| 1 |
| 3 |
| A、f(x1)>0 |
| B、f(x1)<0 |
| C、f(x1)=0 |
| D、f(x1)>0与f(x1)<0均有可能 |
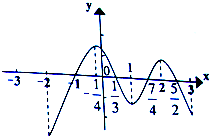 函数y=f(x)在定义域(-2,3)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域(-2,3)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )A、[-1,
| ||||||
B、[-
| ||||||
C、(-2,-
| ||||||
D、(-2,-1]∪[
|
已知函数y=ax2(x≠0)在点(1,a)处切线的倾斜角是45°,则a的值是( )
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
已知数列{an}中,an=n2-n-50,则-8是它的第几项( )
| A、5项 | B、6项 | C、7项 | D、8项 |
执行如图的程序框图,若输入n的值是100,则输出的变量是S与T的差是( )

| A、-50 | B、50 | C、0 | D、10 |