题目内容
在极坐标系(ρ,θ)(ρ≥0,0≤θ<
)中,曲线ρ=4cosθ-
与ρ(cosθ+sinθ)=1的交点的极坐标为 .
| π |
| 2 |
| 3 |
| ρ |
考点:简单曲线的极坐标方程
专题:
分析:把直线与曲线的极坐标方程分别化为直角坐标方程,再联立即可解出.
解答:
解:由ρ(cosθ+sinθ)=1化为直角坐标方程x+y=1.
由曲线ρ=4cosθ-
即ρ2=4ρcosθ-3,化为直角坐标方程x2+y2=4x-3.
联立解方程组
,解得
或
(舍去),
∴交点为(1,0).
∵ρ≥0,0≤θ<
,∴ρ=1,θ=0.
∴交点的极坐标为(1,0).
由曲线ρ=4cosθ-
| 3 |
| ρ |
联立解方程组
|
|
|
∴交点为(1,0).
∵ρ≥0,0≤θ<
| π |
| 2 |
∴交点的极坐标为(1,0).
点评:本题考查了把直线与曲线的极坐标方程化为直角坐标方程、曲线的交点坐标,考查了计算能力,属于基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知函数y=
,y=3x-5,y=lg(x2-4x+3)的定义域分别是P、Q、M,则它们之间的关系是( )
| 1 | ||
|
| A、P?Q?M |
| B、P?M?Q |
| C、Q?M?P |
| D、M?P?Q |
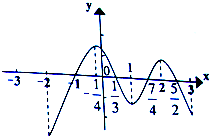 函数y=f(x)在定义域(-2,3)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域(-2,3)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )A、[-1,
| ||||||
B、[-
| ||||||
C、(-2,-
| ||||||
D、(-2,-1]∪[
|
若圆x2+y2-2x=0的圆心到直线x-y+a=0的距离为
,则a的值为( )
| ||
| 2 |
| A、0 | B、-2 |
| C、2或0 | D、0或-2 |