题目内容
若直线ax+by+1=0(a、b>0)过圆x2+y2+8x+2y+1=0的圆心,则
+
的最小值为( )
| 1 |
| a |
| 4 |
| b |
| A、20 | B、16 | C、12 | D、8 |
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:直线过圆心,先求圆心坐标,推出a+b=1,利用1的代换,以及基本不等式求最小值即可.
解答:
解:圆x2+y2+8x+2y+1=0的圆心(-4,-1)在直线ax+by+1=0上,
所以-4a-b+1=0,即 1=4a+b代入,
得
+
=(
+
)(4a+b)=8+
+
≥16 (a>0,b>0当且仅当4a=b时取等号)
则
+
的最小值为16,
故选:B.
所以-4a-b+1=0,即 1=4a+b代入,
得
| 1 |
| a |
| 4 |
| b |
| 1 |
| a |
| 4 |
| b |
| b |
| a |
| 16a |
| b |
则
| 1 |
| a |
| 4 |
| b |
故选:B.
点评:本题考查直线与圆的位置关系,基本不等式,本题关键是利用1的代换后利用基本不等式,考查计算能力,是基础题.

练习册系列答案
相关题目
已知函数y=
,y=3x-5,y=lg(x2-4x+3)的定义域分别是P、Q、M,则它们之间的关系是( )
| 1 | ||
|
| A、P?Q?M |
| B、P?M?Q |
| C、Q?M?P |
| D、M?P?Q |
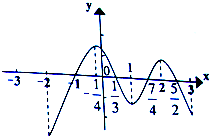 函数y=f(x)在定义域(-2,3)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域(-2,3)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )A、[-1,
| ||||||
B、[-
| ||||||
C、(-2,-
| ||||||
D、(-2,-1]∪[
|
已知函数y=ax2(x≠0)在点(1,a)处切线的倾斜角是45°,则a的值是( )
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
对任意实数x,y,定义运算x*y=ax+by+cxy,其中a,b,c是常数,等式右边的运算是通常的加法和乘法运算.已知1*2=3,2*3=4,并且有一个非零常数m,使得对任意实数x,都有x*m=x,则m的值是( )
| A、-5 | B、-4 | C、4 | D、6 |
已知数列{an}中,an=n2-n-50,则-8是它的第几项( )
| A、5项 | B、6项 | C、7项 | D、8项 |
若圆x2+y2-2x=0的圆心到直线x-y+a=0的距离为
,则a的值为( )
| ||
| 2 |
| A、0 | B、-2 |
| C、2或0 | D、0或-2 |
若sin(α+
)=
,则cos2α=( )
| π |
| 2 |
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|