题目内容
设集合A={x||x-1|<2,x∈Z},B={x|x2-3x+2≤0,x∈Z},则A∩B=( )
| A、(-1,3) |
| B、[1,2] |
| C、{0,1,2} |
| D、{1,2} |
考点:交集及其运算
专题:集合
分析:利用交集性质求解.
解答:
解:∵集合A={x||x-1|<2,x∈Z}={x|-1<x<3,x∈Z}={0,1,2},
B={x|x2-3x+2≤0,x∈Z}={1,2},
∴A∩B={1,2}.
故选:D.
B={x|x2-3x+2≤0,x∈Z}={1,2},
∴A∩B={1,2}.
故选:D.
点评:本题考查交集的求法,是基础题,解题时要注意交集性质的合理运用.

练习册系列答案
相关题目
给出下列四个命题,其中真命题是( )
| A、?x∈R,x2>0 |
| B、?x∈Z,x3<1 |
| C、?x∈N*,x>1 |
| D、?x∈Q,x2=2 |
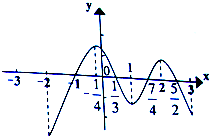 函数y=f(x)在定义域(-2,3)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )
函数y=f(x)在定义域(-2,3)内可导,其图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为( )A、[-1,
| ||||||
B、[-
| ||||||
C、(-2,-
| ||||||
D、(-2,-1]∪[
|
在区间(110,120]内的所有实数中,随机抽取一个实数a,则这个实数a<113的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
对任意实数x,y,定义运算x*y=ax+by+cxy,其中a,b,c是常数,等式右边的运算是通常的加法和乘法运算.已知1*2=3,2*3=4,并且有一个非零常数m,使得对任意实数x,都有x*m=x,则m的值是( )
| A、-5 | B、-4 | C、4 | D、6 |
阅读如图程序框图,运行相应的程序,则输出的结果是( )


A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,对任意的x∈[t,t+2]不等式f(x+t)≥2f(x)恒成立,那么实数t的取值范围是( )
A、[
| ||
| B、[2,+∞) | ||
C、(0,
| ||
D、[0,
|