题目内容
11．已知点A（a，0），点P是双曲线C：$\frac{{x}^{2}}{4}$-y2=1右支上任意一点，若|PA|的最小值为3，则满足条件的A点个数是（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 根据双曲线的性质即可求出．
解答 解：点A（a，0）在x轴上，
点P是双曲线C：$\frac{{x}^{2}}{4}$-y2=1右支上任意一点，|PA|的最小值为3，
点P是双曲线的右顶点，故a的值有2个，
故选：C．
点评 本题考查了双曲线的简单性质，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
2．已知复数z=$\frac{2-i}{1+i}$（i为虚数单位），则在复平面内复数z所对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
6．已知全集U={x∈N|x≤5}，若A={x∈N|2x-5＜0}，则∁UA=（ ）
| A． | {3，4} | B． | {3，4，5} | C． | {2，3，4，5} | D． | {4，5} |
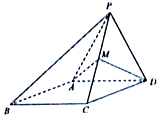如图，四棱锥P-ABCD中，侧面PAD是边长为2的正三角形，且与底面垂直，底面ABCD是菱形，且∠ABC=60°，M为PC的中点．