题目内容
12.已知正项数列{an}中,a1=1,a2=2,$2{a_{n+1}}^2={a_{n+2}}^2+{a_n}^2$,则a6等于( )| A. | 16 | B. | 8 | C. | 4 | D. | $2\sqrt{2}$ |
分析 $2{a_{n+1}}^2={a_{n+2}}^2+{a_n}^2$,可得数列$\{{a}_{n}^{2}\}$为等差数列,利用通项公式即可得出.
解答 解:∵$2{a_{n+1}}^2={a_{n+2}}^2+{a_n}^2$,∴数列$\{{a}_{n}^{2}\}$为等差数列,首项为1,公差为3.
则${a}_{6}^{2}$=1+3×5,a6>0,解得a6=4.
故选:C.
点评 本题考查了等差数列的通项公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
2.已知复数z=$\frac{2-i}{1+i}$(i为虚数单位),则在复平面内复数z所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.已知函数f(x)=Asin(ωx+φ)(A≠0,ω>0,0<φ<$\frac{π}{2}$),若f($\frac{2π}{3}$)=-f(0),则ω的最小值为( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
20.为了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位三十岁到四十岁的公务员,得到如下列联表,因不慎丢失部分数据.
(1))完成表格数据,判断是否有99%以上的把握认为“生二胎意愿与性别有关”并说明理由;
(2)现从有意愿生二胎的45人中随机抽取2人,求男性公务员和女性公务员各一人的概率.
附:k2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
(1))完成表格数据,判断是否有99%以上的把握认为“生二胎意愿与性别有关”并说明理由;
(2)现从有意愿生二胎的45人中随机抽取2人,求男性公务员和女性公务员各一人的概率.
| 男性公务员 | 女性公务员 | 总计 | |
| 有意愿生二胎 | 30 | 15 | 45 |
| 无意愿生二胎 | 20 | 25 | 45 |
| 总计 | 50 | 40 | 90 |
| P(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
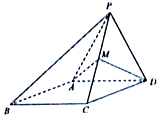 如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.
如图,四棱锥P-ABCD中,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.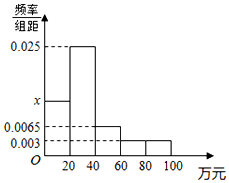 某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为第一组[0,20),第二组AA1⊥平面ABC,第三组[40,60),第四组[60,80),第五组[80,100].
某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为第一组[0,20),第二组AA1⊥平面ABC,第三组[40,60),第四组[60,80),第五组[80,100].