题目内容
3.已知数列{an}的前n项和为Sn,且满足:${a_1}=1,{a_2}=2,{S_n}+1={a_{n+2}}-{a_{n+1}}({n∈{N^*}})$,若不等式λSn>an恒成立,则实数λ的取值范围是λ>1.分析 利用数列的递推关系式转化求解数列是等比数列,然后求解前n项和,以及通项公式公式,然后求出实数λ的取值范围.
解答 解:因${a_1}=1,{a_2}=2,{S_n}+1={a_{n+2}}-{a_{n+1}}({n∈{N^*}})$,
故a3=4,a4=8,
又Sn+1+1=an+3-an+2,
将以上两式两边相减可得an+3=2an+2,则由等比数列的定义可得公比q=2,
所以an=2n-1,Sn=$\frac{1(1-{2}^{n})}{1-2}$=2n-1,
则不等式λSn>an可化为λ>$\frac{{2}^{n-1}}{{2}^{n}-1}$(n≥1),而$\frac{{2}^{n-1}}{{2}^{n}-1}$≤1,
则λ>1.
故答案为:λ>1.
点评 本题考查数列的递推关系式的应用,数列与不等式的关系,考查计算能力.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
13.某射击运动员进行打靶训练,若气枪中有5发子弹,运动员每次击中目标概率均为$\frac{2}{3}$,击中即停止打靶,则运动员所需子弹数的期望为( )
| A. | $\frac{676}{243}$ | B. | $\frac{10}{3}$ | C. | $\frac{121}{81}$ | D. | $\frac{358}{243}$ |
6.若a为实数,$\frac{2+ai}{1+i}$=-2i,则a等于( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
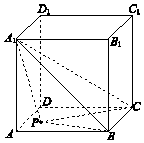 如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$;四面体P-A1BC的体积的最大值是$\frac{4}{3}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$;四面体P-A1BC的体积的最大值是$\frac{4}{3}$. 如图,已知四边形ABCD为正方形,四边形ABEF,四边形DCEF为菱形,且∠AFE=$\frac{π}{3}$,M为BC的中点.
如图,已知四边形ABCD为正方形,四边形ABEF,四边形DCEF为菱形,且∠AFE=$\frac{π}{3}$,M为BC的中点.