题目内容
11.已知当x∈R,[x]表示不超过x的最大整数,称y=[x]为取整函数,例如[1.2]=1,[-2.3]=-3,若f(x)=[x],且偶函数g(x)=-(x-1)2+1(x≥0),则方程f(f(x))=g(x)的所有解之和为-3-$\sqrt{5}$.分析 由偶函数的性质和条件求出x<0时对应的g(x),由[x]的意义和偶函数的图象性质,在同一个坐标系中画出f(f(x))和g(x)的函数图象,根据图象分别求出交点的纵坐标,代入g(x)的解析式求对应的横坐标,即可得到答案.
解答 解:设x<0,则-x>0,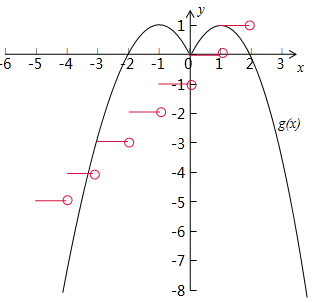
∵偶函数g(x)=-(x-1)2+1(x≥0),
∴g(x)=g(-x)=-(-x-1)2+1
=-(x+1)2+1,
由f(x)=[x]得,f(f(x))=[x],
在同一个坐标系中画出f(f(x))和g(x)的函数图象,如图所示:
由图可得,两个图象有四个交点,交点的纵坐标分为1、0、-3、-4,
当x≥0时,方程f(f(x))=g(x)的解是0和1;
当x<0时,
令g(x)=-(x+1)2+1=-3,解得x=-3,
令g(x)=-(x+1)2+1=-4,解得x=-1-$\sqrt{5}$,
综上得,f(f(x))=g(x)的解是:
0、1、-3、-1-$\sqrt{5}$,
所有解之和是-3-$\sqrt{5}$,
故答案为:$-3-\sqrt{5}$.
点评 本题考查函数奇偶性的图象与性质,取整函数的图象,以及方程根的转化,考查数形结合思想,转化思想,分析问题、解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.复数z1=2+i,若复数z1,z2在复平面内的对应点关于虚轴对称,则z1z2=( )
| A. | -5 | B. | 5 | C. | -3+4i | D. | 3-4i |
15.2017年,嘉积中学即将迎来100周年校庆.为了了解在校同学们对嘉积中学的看法,学校进行了调查,从三个年级任选三个班,同学们对嘉积中学的看法情况如下:
(Ⅰ)从这三个班中各选一个同学,求恰好有2人认为嘉积中学“非常好”的概率(用比例作为相应概率);
(Ⅱ)若在B班按所持态度分层抽样,抽取9人,在这9人中任意选取3人,认为嘉积中学“非常好”的人数记为ξ,求ξ的分布列和数学期望.
| 对嘉积中学的看法 | 非常好,嘉积中学奠定了 我一生成长的起点 | 很好,我的中学很快乐很充实 |
| A班人数比例 | $\frac{1}{2}$ | $\frac{1}{2}$ |
| B班人数比例 | $\frac{2}{3}$ | $\frac{1}{3}$ |
| C班人数比例 | $\frac{3}{4}$ | $\frac{1}{4}$ |
(Ⅱ)若在B班按所持态度分层抽样,抽取9人,在这9人中任意选取3人,认为嘉积中学“非常好”的人数记为ξ,求ξ的分布列和数学期望.