题目内容
9. 如图,已知四边形ABCD为正方形,四边形ABEF,四边形DCEF为菱形,且∠AFE=$\frac{π}{3}$,M为BC的中点.
如图,已知四边形ABCD为正方形,四边形ABEF,四边形DCEF为菱形,且∠AFE=$\frac{π}{3}$,M为BC的中点.(Ⅰ)证明:BC⊥平面MEF;
(Ⅱ)求直线DE与平面MEF所成角的大小.
分析 (I)由BC⊥AB,AB∥EF可得BC⊥EF,由BE=CE得EM⊥BC,从而得出BC⊥平面MEF;
(II)取DA的中点N,连接MN,NF,则DA⊥平面MEF,故∠DEN为直线DE与平面MEF所成角,设AB=1,利用勾股定理计算EN,得出tan∠DEN.
解答 
证明:(I)∵四边形ABCD为正方形,四边形ABEF,四边形DCEF为菱形,
∴AB∥EF,AB⊥BC,BE=EF=CE,
∴BC⊥EF,BC⊥EM,
又EF?平面MEF,EM?平面MEF,EF∩EM=E,
∴BC⊥平面MEF.
解:(II)取DA的中点N,连接MN,NF,
则MN∥AB∥EF,
∴点N∈平面MEF,
∵BC⊥平面MEF,BC∥AD,
∴AD⊥平面MEF,
∴∠DEN为直线DE与平面MEF所成角.
设正方形ABCD的边长AB=1,
∵∠AFE=$\frac{π}{3}$,四边形ABEF是菱形,
∴AE=EF=AB=1,
又AN=DN=$\frac{1}{2}$AD=$\frac{1}{2}$AB=$\frac{1}{2}$,
∴EN=$\sqrt{A{E}^{2}-A{N}^{2}}$=$\frac{\sqrt{3}}{2}$,
∴tan∠DEN=$\frac{DN}{EN}$=$\frac{\sqrt{3}}{3}$,∴∠DEN=$\frac{π}{6}$.
∴直线DE与平面MEF所成角为$\frac{π}{6}$.
点评 本题考查了线面垂直的判定定理,线面角的计算,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知实数x、y满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y≥0\\ x≤1\end{array}\right.$,则z=2x-y的最小值是( )
| A. | -1 | B. | 1 | C. | -3 | D. | 2 |
1.某种商品价格与该商品日需求量之间的几组对照数据如表:
(1)求y关x的线性回归方程;
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程y=bx+a,其中b=$\frac{{x}_{1}{y}_{1}+{x}_{2}{y}_{2}+…{x}_{n}{y}_{n}-n\overline{x}\overline{y}}{{{x}_{1}}^{2}+{{x}_{2}}^{2}+…{{x}_{n}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
| 价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
| 日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程y=bx+a,其中b=$\frac{{x}_{1}{y}_{1}+{x}_{2}{y}_{2}+…{x}_{n}{y}_{n}-n\overline{x}\overline{y}}{{{x}_{1}}^{2}+{{x}_{2}}^{2}+…{{x}_{n}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
18.用反证法证明命题:“若正系数一元二次方程ax2+bx+c=0(a=0)有有理根,那么a,b,c中至多有两个是奇数”时,下列假设中正确的是( )
| A. | 假设a,b,c都是奇数 | B. | 假设a,b,c至少有两个是奇数 | ||
| C. | 假设a,b,c至多有一个是奇数 | D. | 假设a,b,c不都是奇数 |
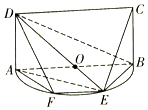 如图,半圆O的直径AB长为2,E是半圆O上除A,B外的一个动点,矩形ABCD所在的平面垂直于该半圆所在的平面,且$tan∠DBA=\frac{1}{2}$,设平面ECD与半圆弧的另一个交点为F.
如图,半圆O的直径AB长为2,E是半圆O上除A,B外的一个动点,矩形ABCD所在的平面垂直于该半圆所在的平面,且$tan∠DBA=\frac{1}{2}$,设平面ECD与半圆弧的另一个交点为F.