题目内容
18.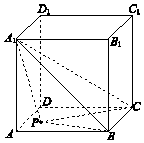 如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$;四面体P-A1BC的体积的最大值是$\frac{4}{3}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P在正方形ABCD的边界及其内部运动.平面区域W由所有满足${A_1}P≤\sqrt{5}$的点P组成,则W的面积是$\frac{π}{4}$;四面体P-A1BC的体积的最大值是$\frac{4}{3}$.
分析 由已知可得平面区域W是以A为圆心,以1为半径的$\frac{1}{4}$圆面,由圆的面积公式求得W的面积;由题意可得,当p在边AD上时,四面体P-A1BC的体积有最大值,再由棱锥体积公式求解.
解答 解:连接AP,则A1A⊥AP,
∵A1A=2,${A}_{1}P=\sqrt{5}$,∴AP=1,
以A为圆心,以1为半径作圆交正方形ABCD所得$\frac{1}{4}$圆,
∴W的面积是$\frac{1}{4}×π×{1}^{2}=\frac{π}{4}$;
由题意可知,当p在边AD上时,四面体P-A1BC的体积的最大值是$\frac{1}{3}×\frac{1}{2}×2×2×2=\frac{4}{3}$.
故答案为:$\frac{π}{4}$;$\frac{4}{3}$.
点评 本题考查棱柱的结构特征,考查了空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
9.设x,y满足约束条件$\left\{\begin{array}{l}8x-y-4≤0\\ x+y+1≥0\\ y-4x≤0\end{array}\right.$,目标函数z=ax+by(a>0,b>0)的最大值为2,则$\frac{1}{a}+\frac{1}{b}$的最小值为( )
| A. | 5 | B. | $\frac{5}{2}$ | C. | $\frac{9}{2}$ | D. | 9 |
4.已知实数x、y满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y≥0\\ x≤1\end{array}\right.$,则z=2x-y的最小值是( )
| A. | -1 | B. | 1 | C. | -3 | D. | 2 |
1.某种商品价格与该商品日需求量之间的几组对照数据如表:
(1)求y关x的线性回归方程;
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程y=bx+a,其中b=$\frac{{x}_{1}{y}_{1}+{x}_{2}{y}_{2}+…{x}_{n}{y}_{n}-n\overline{x}\overline{y}}{{{x}_{1}}^{2}+{{x}_{2}}^{2}+…{{x}_{n}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
| 价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
| 日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程y=bx+a,其中b=$\frac{{x}_{1}{y}_{1}+{x}_{2}{y}_{2}+…{x}_{n}{y}_{n}-n\overline{x}\overline{y}}{{{x}_{1}}^{2}+{{x}_{2}}^{2}+…{{x}_{n}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
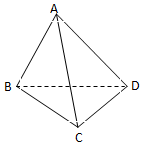 如图,在三棱锥A-BCD中,已知,∠BAC=60°,BD=DC=$\sqrt{2}$,AB=AC=AD=2.
如图,在三棱锥A-BCD中,已知,∠BAC=60°,BD=DC=$\sqrt{2}$,AB=AC=AD=2.