题目内容
设P为锐角△ABC的外心(三角形外接圆圆心),
=k(
+
)(k∈R).若cos∠BAC=
,则k=( )
| AP |
| AB |
| AC |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:如图所示,取BC的中点D,连接PD,AD.可得PD⊥BC,
+
=2
.由满足
=k(
+
)(k∈R),可得
=2K
,A,P,D三点共线,得到AB=AC.因此cos∠BAC=cos∠DPC=
=
=
.即可得出.
| AB |
| AC |
| AD |
| AP |
| AB |
| AC |
| AP |
| AD |
| DP |
| PC |
| DP |
| PA |
| 2 |
| 5 |
解答:
解:如图所示,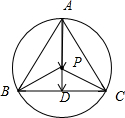
取BC的中点D,连接PD,AD.
则PD⊥BC,
+
=2
,
∵满足
=k(
+
)(k∈R
∴
=2K
,
∴A,P,D三点共线,
∴AB=AC.
∴cos∠BAC=cos∠DPC=
=
=
.
∴AP=
AD.
∴2k=
,
解得k=
.
故选:A.

取BC的中点D,连接PD,AD.
则PD⊥BC,
| AB |
| AC |
| AD |
∵满足
| AP |
| AB |
| AC |
∴
| AP |
| AD |
∴A,P,D三点共线,
∴AB=AC.
∴cos∠BAC=cos∠DPC=
| DP |
| PC |
| DP |
| PA |
| 2 |
| 5 |
∴AP=
| 5 |
| 7 |
∴2k=
| 5 |
| 7 |
解得k=
| 5 |
| 14 |
故选:A.
点评:本题考查了向量共线定理、直角三角形的边角关系、三角形外心性质、向量平行四边形法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
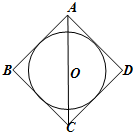 如图,在正方形ABCD内作内切圆O,将正方形ABCD、圆O绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )
如图,在正方形ABCD内作内切圆O,将正方形ABCD、圆O绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )A、2:
| ||
B、2
| ||
C、2:
| ||
D、
|
圆锥的母线长为2,侧面展开图是一个半圆,则此圆锥的表面积为( )
| A、6π | B、5π | C、3π | D、2π |
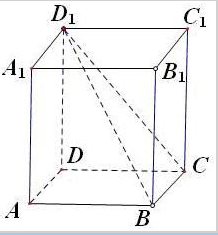 设正方体ABCD-A1B1C1D1的棱长为1,则:
设正方体ABCD-A1B1C1D1的棱长为1,则: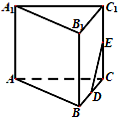 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.AA1=1,AC=
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.AA1=1,AC=
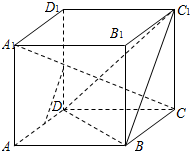 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AD,DD1中点.求证:(1)EF∥平面C1BD;
如图,在正方体ABCD-A1B1C1D1中,E,F分别是AD,DD1中点.求证:(1)EF∥平面C1BD;