题目内容
已知函数f(x)=
,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是 .
|
考点:分段函数的应用
专题:计算题,函数的性质及应用
分析:由题意,f(x)在(0,2]上先减后增,在(2,+∞)单调递减,从而判断出a,b,c在(0,2]上有两个,在(2,+∞)上有一个,从而可推出ab=1,将abc的取值范围化为c的取值范围,从而求c的取值范围.
解答:
解:∵f(x)=
,
∴f(x)在(0,2]上先减后增,在(2,+∞)单调递减,
又∵a,b,c互不相等,
∴a,b,c在(0,2]上有两个,在(2,+∞)上有一个,
不妨设a,b∈(0,2],c∈(2,+∞),
则log2a+log2b=0,
即ab=1,
则abc的取值范围是c的取值范围,
∵在(0,2]上,f(x)由+∞→0→1,
则0<f(c)≤1,
即0<-
c+4≤1,
解得,6≤c<8.
故答案为:[6,8).
|
∴f(x)在(0,2]上先减后增,在(2,+∞)单调递减,
又∵a,b,c互不相等,
∴a,b,c在(0,2]上有两个,在(2,+∞)上有一个,
不妨设a,b∈(0,2],c∈(2,+∞),
则log2a+log2b=0,
即ab=1,
则abc的取值范围是c的取值范围,
∵在(0,2]上,f(x)由+∞→0→1,
则0<f(c)≤1,
即0<-
| 1 |
| 2 |
解得,6≤c<8.
故答案为:[6,8).
点评:本题考查了分段函数的应用,同时考查了函数的单调性与函数的值的关系,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知F1、F2分别是椭圆M:
+
=1(a>
)的左右焦点,点P是椭圆M上一点,且
•
=0,则离心率e取最小值时椭圆M的方程为( )
| x2 |
| a2 |
| y2 |
| a2-2 |
| 2 |
| PF1 |
| PF2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列终边相同的是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、(2k+1)π,(4k+1)π,k∈Z |
圆O1:x2+y2-2x=0和圆O2:x2+y2-4y=0的公共弦长为( )
A、
| ||||
B、
| ||||
| C、3 | ||||
D、
|
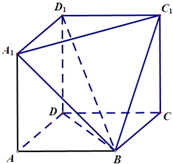 如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.
如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.