题目内容
7.一个车间为了规定工时定额,需要确定加工零件所花费的时间,由此进行了5次实验,收集数据如下:| 零件数:x个 | 10 | 20 | 30 | 40 | 50 |
| 加工时间:y分钟 | 59 | 71 | 75 | 81 | 89 |
附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| A. | 124分钟 | B. | 150分钟 | C. | 162分钟 | D. | 178分钟 |
分析 根据表中数据,计算$\overline{x}$、$\overline{y}$,求出回归系数,写出线性回归方程,利用回归方程计算x=100时$\stackrel{∧}{y}$的值即可.
解答 解:根据表中数据,计算
$\overline{x}$=$\frac{1}{5}$×(10+20+30+40+50)=30,
$\overline{y}$=$\frac{1}{5}$×(59+71+75+81+89)=75,
∴$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$
=$\frac{(-20)×(-16)+(-10)×(-4)+0×0+10×6+20×14}{{(-20)}^{2}{+(-10)}^{2}{+0}^{2}{+10}^{2}{+20}^{2}}$
=$\frac{700}{1000}$
=0.7,
$\widehata=\overline y-\widehatb\overline x$=75-0.7×30=54;
∴y关于x的线性回归方程是$\stackrel{∧}{y}$=0.7x+54,
当x=100时,$\stackrel{∧}{y}$=0.7×100+54=124(分钟).
故选:A.
点评 本小题考查了线性回归方程的求法与应用问题,是基础题目.

练习册系列答案
相关题目
1.已知$λ=3\int_0^1{{x^2}dx}$,在矩形ABCD中,AB=2,AD=1,点P为矩形ABCD内一点,则使得$\overrightarrow{AP}•\overrightarrow{AC}≥λ$的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
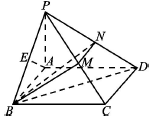 如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥BC.
如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥BC.