题目内容
18.已知点M(a,b)在直线3x+4y-20=0上,则$\sqrt{{a^2}+{b^2}}$的最小值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 考虑a2+b2的几何意义,利用转化思想,求出原点到直线3x+4y-20=0的距离即可.
解答 解:∵点M(a,b)在直线3x+4y-20=0上,
则$\sqrt{{a^2}+{b^2}}$的几何意义是点M(a,b)到原点的距离,
而原点到直线的距离d=$\frac{20}{\sqrt{{3}^{2}+{4}^{2}}}$=4,
则$\sqrt{{a^2}+{b^2}}$的最小值为:4.
故选:B.
点评 本题考查点到直线的距离公式,也利用利用二次函数的性质求解,考查计算能力,是基础题.

练习册系列答案
相关题目
8.口袋中装有一些大小相同的红球、白球和黑球,从中摸出一个球,摸出红球的概率是0.43,摸出白球的概率是0.27,那么摸出黑球的概率是( )
| A. | 0.43 | B. | 0.27 | C. | 0.3 | D. | 0.7 |
13.设l,m,n表示三条直线,α,β,γ表示三个平面,则下面命题中不成立的是( )
| A. | 若l⊥α.m⊥α,则l∥m | |
| B. | 若m?β,m⊥l,n是l在β内的射影,则m⊥n | |
| C. | 若m?α,n?α,m∥n,则n∥α | |
| D. | 若α⊥γ,β⊥γ,则α∥β. |
10.书架上有2本不同的语文书,1本数学书,从中任意取出2本,取出的书恰好都是语文书的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
7.一个车间为了规定工时定额,需要确定加工零件所花费的时间,由此进行了5次实验,收集数据如下:
由以上数据的线性回归方程估计加工100个零件所花费的时间为( )
附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| 零件数:x个 | 10 | 20 | 30 | 40 | 50 |
| 加工时间:y分钟 | 59 | 71 | 75 | 81 | 89 |
附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| A. | 124分钟 | B. | 150分钟 | C. | 162分钟 | D. | 178分钟 |
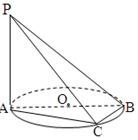 已知AB是圆O的直径,C为底面圆周上一点,PA⊥平面ABC,
已知AB是圆O的直径,C为底面圆周上一点,PA⊥平面ABC,