题目内容
1.△ABC中,角A,B,C所对的边分别为a,b,c,已知A=60°,b=2,S△ABC=2$\sqrt{3}$,则$\frac{a+b+c}{sinA+sinB+sinC}$=4.分析 首先利用三角形的面积公式求出c的长度,进一步利用余弦定理求出a的长度,在应用正弦定理和等比性质求出结果.
解答 解:已知∠A=60°,b=2,面积S△ABC=2$\sqrt{3}$,
S=$\frac{1}{2}$bcsinA=2$\sqrt{3}$,
解得:c=4,
利用余弦定理:a2=b2+c2-2bccosA,
解得:a=2$\sqrt{3}$,
利用正弦定理:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4,
利用等比性质:则$\frac{a+b+c}{sinA+sinB+sinC}$=4,
故答案为:4.
点评 本题考查的知识点:三角形的面积公式,余弦定理和正弦定理的应用,等比性质的应用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
16.已知直线y=kx+1与曲线y=x3+mx+n相切于点P(1,3),则n=( )
| A. | -1 | B. | 1 | C. | 3 | D. | 4 |
9.若等比数列{an}满足a2•a4=$\frac{1}{2}$,则a1a32a5=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
16.已知集合P={x∈N|1≤x<10},集合Q={x∈R|x2+x-6=0},则P∩Q=( )
| A. | {2} | B. | {3} | C. | {-2,3} | D. | .{-3,2} |
13.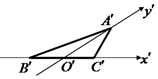 如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=$\sqrt{6}$,A′O′=$\frac{\sqrt{3}}{4}$,那么△ABC的面积是( )
如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=$\sqrt{6}$,A′O′=$\frac{\sqrt{3}}{4}$,那么△ABC的面积是( )
 如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=$\sqrt{6}$,A′O′=$\frac{\sqrt{3}}{4}$,那么△ABC的面积是( )
如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=$\sqrt{6}$,A′O′=$\frac{\sqrt{3}}{4}$,那么△ABC的面积是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 3$\sqrt{2}$ |
10.在锐角△ABC中,sinA=$\frac{2\sqrt{6}}{5}$,cosC=$\frac{5}{7}$,BC=7,若动点P满足$\overrightarrow{AP}$=$\frac{λ}{2}$$\overrightarrow{AB}$+(1-λ)$\overrightarrow{AC}$(λ∈R),则点P轨迹与直线AB,AC所围成的封闭区域的面积( )
| A. | 3$\sqrt{6}$ | B. | 4$\sqrt{6}$ | C. | 6$\sqrt{6}$ | D. | 12$\sqrt{6}$ |
11.下列各组函数中,表示同一函数的是( )
| A. | y=1,y=$\frac{x}{x}$ | B. | y=$\frac{{x}^{2}-x}{x}$与y=x-1 | C. | y=x,y=$\root{3}{{x}^{3}}$ | D. | y=|x|,y=($\sqrt{x}$)2 |