题目内容
已知函数f(x)=
(ax-a-x),g(x)=
(ax+a-x),求证:[f(x)]2+[g(x)]2=g(2x).
| 1 |
| 2 |
| 1 |
| 2 |
考点:指数函数综合题
专题:函数的性质及应用
分析:由已知中,函数f(x)=
(ax-a-x),g(x)=
(ax+a-x),结合对数的运算性质,代入化简:[f(x)]2+[g(x)]2,可得结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
证明:∵函数f(x)=
(ax-a-x),g(x)=
(ax+a-x),
∴[f(x)]2+[g(x)]2=
(ax-a-x)2+
(ax+a-x)2=
(2a2x+2a-2x)=
(a2x+a-2x)=g(2x).
即:[f(x)]2+[g(x)]2=g(2x).
| 1 |
| 2 |
| 1 |
| 2 |
∴[f(x)]2+[g(x)]2=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
即:[f(x)]2+[g(x)]2=g(2x).
点评:本题考查的知识点是指数的运算性质,难度不大,属于基础题.

练习册系列答案
相关题目
函数f(x)=-x2-4x+1(-3≤x≤3)的值域是( )
| A、(-4,5] |
| B、[-20,4] |
| C、[-20,5] |
| D、[4,5] |
函数f(x)=cosx-
sinx的一条对称轴方程是( )
| 3 |
A、x=
| ||
B、x=
| ||
C、x=-
| ||
D、x=
|
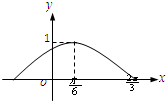
已知函数f(x)=sin(ωx+φ)(ω>0,-
<φ<
),其部分图象如图所示,则ω,φ的值分别为( )
| π |
| 2 |
| π |
| 2 |

A、ω=2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=
| ||
D、ω=1,φ=
|
设M={x|x2+x+2=0},a=0,则{a}与M的关系是( )
| A、{a}=M |
| B、M?{a} |
| C、{a}?M |
| D、M?{a} |