题目内容
若函数f（x）=
的定义域[1，+∞），则a的取值范围是 ．
| 2x-a |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：把函数f（x）=
的定义域为[1，+∞）转化为2x-a≥0的解集为[1，+∞），求解不等式后解对数方程得答案．
| 2x-a |
解答：
解：∵函数f（x）=
的定义域为[1，+∞），
∴2x-a≥0的解集为[1，+∞），
由2x-a≥0，得x≥log2a，
则log2a=1，即a=2．
故答案为：2．
| 2x-a |
∴2x-a≥0的解集为[1，+∞），
由2x-a≥0，得x≥log2a，
则log2a=1，即a=2．
故答案为：2．
点评：本题考查了函数的定义域及其求法，考查了数学转化思想方法，是基础题．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
设集合A={x|
＜2x＜4}，B={x|x2≤1}，则A∪B=（ ）
| 1 |
| 2 |
| A、{x|x＜2} | ||
B、{x|-
| ||
| C、{x|-1≤x＜2} | ||
| D、{x|1≤x＜2} |
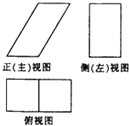一个几何体的三视图如图所示，已知正（主）视图是底边长为1的平行四边形，侧（左）视图是一个长为