题目内容
已知z是复数,z-3i,
均为实数,(i为虚单位),求复数z.
| 1+z |
| 2i |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:设z=a+bi(a,b∈R),利用两复数为实数的概念可求得a与b,从而可得答案.
解答:
解:设z=a+bi(a,b∈R),则z-3i=a+(b-3)i,
又
=
=
-
(a+1)i,
∵z-3i,
均为实数,
∴
,
解得:
,
∴z=-1+3i.
又
| 1+z |
| 2i |
| (a+1)+bi |
| 2i |
| b |
| 2 |
| 1 |
| 2 |
∵z-3i,
| 1+z |
| 2i |
∴
|
解得:
|
∴z=-1+3i.
点评:本题考查复数代数形式的乘除运算,考查复数是实数的条件的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.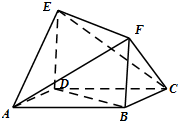 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD, 已知一几何体的三视图如图所示,点F,G分别为AC,DE的中点.
已知一几何体的三视图如图所示,点F,G分别为AC,DE的中点.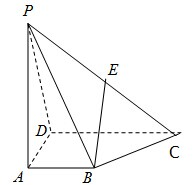 如图,在四棱锥P-ABCD中,AB∥DC,DC=2AB,E为PC的中点.
如图,在四棱锥P-ABCD中,AB∥DC,DC=2AB,E为PC的中点.