题目内容
已知等差数列25,21,17…,求通项公式an,并求前n项和Sn的最大值.
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:等差数列25,21,17…中,a1=25,d=21-25=-4,由此求出an=29-4n.Sn=-2n2+27n,利用配方法能求出前n项和Sn的最大值.
解答:
解:等差数列25,21,17…中,
a1=25,d=21-25=-4,
∴an=25+(n-1)×(-4)=29-4n.
Sn=25n+
×(-4)
=-2n2+27n
=-2(n2-
n)
=-2(n-
)2+
,
∴n=7时,Sn最大值S7=-2×
+
=91.
∴前n项和Sn的最大值为91.
a1=25,d=21-25=-4,
∴an=25+(n-1)×(-4)=29-4n.
Sn=25n+
| n(n-1) |
| 2 |
=-2n2+27n
=-2(n2-
| 27 |
| 2 |
=-2(n-
| 27 |
| 4 |
| 729 |
| 8 |
∴n=7时,Sn最大值S7=-2×
| 1 |
| 16 |
| 729 |
| 8 |
∴前n项和Sn的最大值为91.
点评:本题考查等差数列的通项公式和前n项和的最大值的求法,是基础题,解题时要注意配方法的合理运用.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
若x>1,则x+
的最小值是( )
| 1 |
| x-1 |
| A、1 | B、2 | C、3 | D、4 |
 如图,在等腰直角△ABC中,AB=AC=3,点D在边BC上且BD=
如图,在等腰直角△ABC中,AB=AC=3,点D在边BC上且BD=| 1 |
| 2 |
| AP |
| CP |
A、[-
| ||
B、[-
| ||
C、[
| ||
D、[0,
|
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、55 | ||
| B、54 | ||
C、75+4
| ||
D、55+2
|
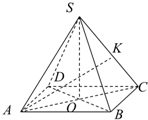 如图,设S-ABCD是一个高为3的四棱锥,底面ABCD是边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心.K是棱SC的中点.试求直线AK与平面SBC所成角的大小.
如图,设S-ABCD是一个高为3的四棱锥,底面ABCD是边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心.K是棱SC的中点.试求直线AK与平面SBC所成角的大小.