题目内容
已知F1、F2是椭圆C:
+
=1(a>b>0)的左、右交点,点P(-
,1)在椭圆上,线段PF2与y轴的交点M满足
+
=
.
(1)求椭圆的标准方程;
(2)设A、B是椭圆上的动点,直线OA与OB的斜率乘积kOA•kOB=-
,动点N满足
=
+λ
(其中实数λ为常数),问是否存在两个定点Q1、Q2,使得|NQ1|+|NQ2|=8?若存在,求Q1、Q2的坐标及λ的值;若不存在,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| PM |
| F2M |
| 0 |
(1)求椭圆的标准方程;
(2)设A、B是椭圆上的动点,直线OA与OB的斜率乘积kOA•kOB=-
| 1 |
| 2 |
| ON |
| OA |
| OB |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)根据题意,列出方程组
,求出a2、b2,得椭圆的方程;
(2)设出N(x,y),A(x1,y1),B(x2,y2),根据题意求出N点的轨迹是椭圆
+
=1,
设出该椭圆的左、右焦点Q1,Q2,由椭圆的定义知|NQ1|+|NQ2|为定值;令定值等于8,求出λ的值,即可求出存在的定点Q1、Q2.
|
(2)设出N(x,y),A(x1,y1),B(x2,y2),根据题意求出N点的轨迹是椭圆
| x2 |
| 4+4λ2 |
| y2 |
| 2+2λ2 |
设出该椭圆的左、右焦点Q1,Q2,由椭圆的定义知|NQ1|+|NQ2|为定值;令定值等于8,求出λ的值,即可求出存在的定点Q1、Q2.
解答:
解:(1)∵点P(-
,1)在椭圆上,
∴
+
=1①,
又∵线段PF2与y轴的交点M满足
+
=
,
∴M为线段PF2的中点,
∴-
+c=0②,
又a2=b2+c2③,
①②③联立
,
解得a2=4,b2=c2=2,
∴椭圆C的方程为
+
=1;
(2)设N(x,y),A(x1,y1),B(x2,y2),
∵
=
+λ
,
∴(x,y)=(x1,y1)+λ(x2,y2)=(x1+λx2,y1+λy2),
即x=x1+λx2,y=y1+λy2;
又∵点A、B在椭圆
+
=1上,
∴x12+2y12=4,x22+2y22=4,
∴x2+2y2=(x12+λ2x22+2λx1x2)+2(y12+λ2y22+2λy1y2)
=(x12+2y12)+λ2(x22+2y22)+2λ(x1x2+2y1y2)
=4+4λ2+2λ(x1x2+2y1y2);
又∵kOA•kOB=
•
=-
,
∴x1x2+2y1y2=0,
∴x2+2y2=4+4λ2;
即
+
=1,
∴N点是椭圆
+
=1上的点,
设该椭圆的左、右焦点为Q1,Q2,
由椭圆的定义知,|NQ1|+|NQ2|为定值;
又∵c2=2+2λ2,
∴此椭圆的两焦点的坐标为Q1(-
,0),Q2(
,0);
令|NQ1|+|NQ2|=2(
)=8,
解得λ=±
,
∴存在两个定点Q1(-2
,0),Q2(2
,0),
使得|NQ1|+|NQ2|=8,此时λ=±
.
| 2 |
∴
| 2 |
| a2 |
| 1 |
| b2 |
又∵线段PF2与y轴的交点M满足
| PM |
| F2M |
| 0 |
∴M为线段PF2的中点,
∴-
| 2 |
又a2=b2+c2③,
①②③联立
|
解得a2=4,b2=c2=2,
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 2 |
(2)设N(x,y),A(x1,y1),B(x2,y2),
∵
| ON |
| OA |
| OB |
∴(x,y)=(x1,y1)+λ(x2,y2)=(x1+λx2,y1+λy2),
即x=x1+λx2,y=y1+λy2;
又∵点A、B在椭圆
| x2 |
| 4 |
| y2 |
| 2 |
∴x12+2y12=4,x22+2y22=4,
∴x2+2y2=(x12+λ2x22+2λx1x2)+2(y12+λ2y22+2λy1y2)
=(x12+2y12)+λ2(x22+2y22)+2λ(x1x2+2y1y2)
=4+4λ2+2λ(x1x2+2y1y2);
又∵kOA•kOB=
| y1 |
| x1 |
| y2 |
| x2 |
| 1 |
| 2 |
∴x1x2+2y1y2=0,
∴x2+2y2=4+4λ2;
即
| x2 |
| 4+4λ2 |
| y2 |
| 2+2λ2 |
∴N点是椭圆
| x2 |
| 4+4λ2 |
| y2 |
| 2+2λ2 |
设该椭圆的左、右焦点为Q1,Q2,
由椭圆的定义知,|NQ1|+|NQ2|为定值;
又∵c2=2+2λ2,
∴此椭圆的两焦点的坐标为Q1(-
| 2+2λ2 |
| 2+2λ2 |
令|NQ1|+|NQ2|=2(
| 4+4λ2 |
解得λ=±
| 3 |
∴存在两个定点Q1(-2
| 2 |
| 2 |
使得|NQ1|+|NQ2|=8,此时λ=±
| 3 |
点评:本题考查了椭圆的标准方程及其性质、点在椭圆上满足椭圆的方程、斜率计算公式等基础知识与基本技能方法,考查了推理和计算能力,是难题.

练习册系列答案
相关题目
计算sin137°cos13°-cos(-43°)cos77°的结果等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线
-
=1(a>0,b>0)的离心率为
,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A、y=±
| ||||
B、y=±
| ||||
| C、y=±2x | ||||
D、y=±
|
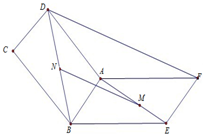 如图,已知ABCD与ABEF是两个平行四边形且不共面,M、N分别为AE、BD中点,求证:MN∥平面DAF.
如图,已知ABCD与ABEF是两个平行四边形且不共面,M、N分别为AE、BD中点,求证:MN∥平面DAF.