题目内容
7.已知函数f(x)=x2(x-3a)+1(a>0,x∈R)(1)求函数y=f(x)的极值;
(2)函数y=f(x)在(0,2)上单调递减,求实数a的取值范围;
(3)若在区间(0,+∞)上存在实数x0,使得不等式f(x0)-4a3≤0能成立,求实数a的取值范围.
分析 (1)求导,根据导数与函数单调性及极值的关系,即可求得函数y=f(x)的极值;
(2)由(1)可知:函数y=f(x)在(0,2)上单调递减,则2a≥2,即可求得a的取值范围;
(3)由题意可知:-4a3≥f(x) min在(0,+∞)上恒成立,由(1)可知:f(x)的最小值为:-4a3+1,即可求得实数a的取值范围.
解答 解:(1)f(x)=x2(x-3a)+1,求导f'(x)=3x(x-2a),令 f'(x)=0,解得x=0或 x=2a.
f(0)=1,f(2a)=-4a3+1.
当a>0时,2a>0,当 x变化时,f'(x),f(x)的变化情况如下表:
| x | (-∞,0) | 0 | (0,2a) | 2a | (2a,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 1 | ↘ | -4a3+1 | ↗ |
(2)在(0,2)上单调递减,∴2a≥2,即a≥1,
实数a的取值范围[1,+∞);
(3)依题意在区间(0,+∞)上存在实数x0,得使得不等式f(x0)-4a3≤0能成立,则4a3≥f(x0)在(0,+∞)上成立,
∴4a3≥f(x)min,由(1)可知:f(x)的最小值为:-4a3+1,
∴4a3≥-4a3+1,则8a3≥1,
解得:a≥$\frac{1}{2}$,
∴实数a的取值范围[$\frac{1}{2}$,+∞).
点评 本题考查导数的综合应用,考查导数与函数单调性的关系,利用导数求函数的单调性及极值,考查不等式恒成立,考查转化思想,属于中档题.

练习册系列答案
相关题目
19.已知变量x、y满足约束条件$\left\{\begin{array}{l}{x+y-3≥0}\\{x-2y+3≥0}\\{x≤a}\end{array}\right.$,且z=x+2y的最小值为3,则$\frac{y}{x+1}$≥$\frac{1}{2}$的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{9}$ |
16.函数$f(x)=\frac{1}{x}{log_2}({{4^x}+1})-1$的图象( )
| A. | 关于原点对称 | B. | 关于y轴对称 | C. | 关于x轴对称 | D. | 关于直线y=x对称 |
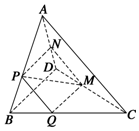 如图,在四面体ABCD中,截面PQMN是正方形,则下列命题中,正确的为①②④(填序号).
如图,在四面体ABCD中,截面PQMN是正方形,则下列命题中,正确的为①②④(填序号).