题目内容
18.设f(x)=$\frac{1}{3}$x3+3x2+ax,若g(x)=$\frac{1}{{4}^{x}}$,对任意x1∈[$\frac{1}{2}$,1],存在x2∈[$\frac{1}{2}$,2],使得f′(x1)≤g(x2)成立,则实数a的取值范围为(-∞,-$\frac{13}{2}$].分析 先将问题等价为:f'(x)max≤g(x)max,再分别对二次函数和指数函数在相应区间上求最值.
解答 解:根据题意,要使得f'(x1)≤g(x2)成立,
只需满足:f'(x)max≤g(x)max,
而f'(x)=x2+6x+a=(x+3)2+a-9,x∈[$\frac{1}{2}$,1],
所以,f'(x)max=f(1)=a+7,
g(x)=$\frac{1}{4^x}$,x∈[$\frac{1}{2}$,2],函数单调递减,
所以,g(x)max=g($\frac{1}{2}$)=$\frac{1}{2}$,
因此,a+7≤$\frac{1}{2}$,解得a≤-$\frac{13}{2}$,
所以,实数a的取值范围为:(-∞,-$\frac{13}{2}$],
故答案为:(-∞,-$\frac{13}{2}$].
点评 本题主要考查了不等式有解和恒成立的综合问题,涉及二次函数和指数函数的单调性和值域,以及导数的运算,属于中档题.

练习册系列答案
相关题目
10.已知全集U=R,集合A=$\left\{{x|y=\frac{1}{lnx}}\right\}$,B=$\left\{{x|y=\sqrt{-{x^2}+x}}\right\}$,则(∁UA)∩B=( )
| A. | {0} | B. | {0,1} | C. | ∅ | D. | (0,1) |
7.已知P为直线y=kx+b上一动点,若点P与原点均在直线x-y+2=0的同侧,则k,b满足的条件分别为( )
| A. | k=1,b<2 | B. | k=1,b>2 | C. | k≠1,b<2 | D. | k≠1,b>2 |
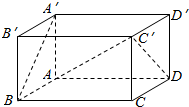 如图,长方体ABCD-A′B′C′D′中,AD=2AB=2AA′=2.
如图,长方体ABCD-A′B′C′D′中,AD=2AB=2AA′=2.