题目内容
3.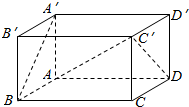 如图,长方体ABCD-A′B′C′D′中,AD=2AB=2AA′=2.
如图,长方体ABCD-A′B′C′D′中,AD=2AB=2AA′=2.(1)求证:A′B⊥平面ADC′;
(2)求二面角D′-AC-D的正切值.
分析 (1)连接AB′,证明A′B⊥C′D,A′B⊥AD,即可证明A′B⊥平面ADC′;
(2)过D作DE⊥AC,垂足为E,连接D′E,则∠D′ED为二面角D′-AC-D的平面角,求出DE,即可求二面角D′-AC-D的正切值.
解答 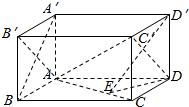 (1)证明:连接AB′,
(1)证明:连接AB′,
∵长方体ABCD-A′B′C′D′中,AB=AA′,
∴A′B⊥AB′,
∴A′B⊥C′D,
∵A′B⊥AD,AD∩C′D=D,
∴A′B⊥平面ADC′;
(2)解:过D作DE⊥AC,垂足为E,连接D′E,则∠D′ED为二面角D′-AC-D的平面角.
△ACD中,由等面积可得DE=$\frac{2×1}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
∵DD′=1,
∴二面角D′-AC-D的正切值=$\frac{1}{\frac{2\sqrt{5}}{5}}$=$\frac{\sqrt{5}}{2}$.
点评 本题考查线面垂直的证明,考查二面角D′-AC-D的正切值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
11.直线y=kx+1与圆x2+y2=1的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相交或相切 | D. | 不能确定 |
13.下列函数中,既是偶函数又在区间(0,$\frac{π}{2}$)上单调递增的函数是( )
| A. | y=-sinx | B. | y=-cosx | C. | y=sin2x | D. | y=cos2x |