题目内容
3．下列函数中，在其定义域内既是奇函数又是增函数的是（ ）| A． | y=x+x3 | B． | y=3x | C． | y=log2x | D． | $y=-\frac{1}{x}$ |
分析 求出各项中函数的导函数，根据导函数的正负对于增减性做出判断，再利用函数的奇偶性判断即可．
解答 解：y′=x2+1＞0，即函数为增函数，
∵f（-x）=-x-x3=-f（x），
∴函数为偶函数，
故选：A．
点评 此题考查了函数单调性的判断与证明，函数奇偶性的判断，熟练掌握函数的性质是解本题的关键．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
13．已知向量$\overrightarrow{a}$=（$\sqrt{3}$，1），$\overrightarrow{b}$=（m，1）．若向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为$\frac{2π}{3}$，则实数m=（ ）
| A． | -$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | -$\sqrt{3}$或0 | D． | 2 |
14．已知抛物线y2=2px（p＞0）与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;（a＞0，b＞0）$有相同的焦点F，点A是两曲线的一个交点，且AF⊥x轴，若l为双曲线一、三象限的一条渐近线，则l的倾斜角所在的区间可能是（ ）
| A． | $（{0，\frac{π}{6}}）$ | B． | $（{\frac{π}{6}，\frac{π}{4}}）$ | C． | $（{\frac{π}{4}，\frac{π}{3}}）$ | D． | $（{\frac{π}{3}，\frac{π}{2}}）$ |
11．设a＞0，b＞0．若$\sqrt{3}$是3a与3b的等比中项，则ab的最大值为（ ）
| A． | 8 | B． | 4 | C． | 1 | D． | $\frac{1}{4}$ |
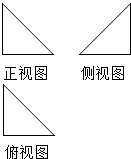一个空间几何体的三视图如图所示，其正视图、侧视 图、俯视图均为等腰直角三角形，且直角边长都为1，则它的外接球的表面积是（ ）
8．直线x+y-2=0与直线x-y+3=0的位置关系是（ ）
| A． | 平行 | B． | 垂直 | C． | 相交但不垂直 | D． | 不能确定 |